如图,四棱锥 中,侧面PAD为等边三角形且垂直于底面ABCD, , .
(1)证明:直线BC∥平面PAD;
(2)若△PCD面积为 ,求四棱锥 的体积.
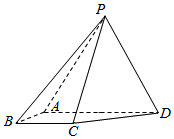
如图,三棱锥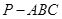 中,
中, ,
,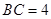 ,
,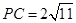 ,点
,点 在平面
在平面 内的射影恰为
内的射影恰为 的重心
的重心 ,M为侧棱
,M为侧棱 上一动点.
上一动点.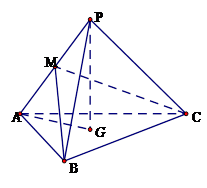
(1)求证:平面 平面
平面 ;
;
(2)当M为 的中点时,求直线
的中点时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
江西某品牌豆腐食品是经过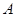 、
、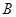 、
、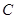 三道工序加工而成的,
三道工序加工而成的,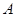 、
、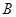 、
、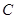 工序的产品合格率分别为
工序的产品合格率分别为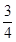 、
、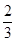 、
、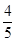 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
(1)生产一袋豆腐食品,求产品为废品的概率;
(2)生产一袋豆腐食品,设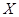 为三道加工工序中产品合格的工序数,求
为三道加工工序中产品合格的工序数,求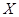 的分布列和数学期望.
的分布列和数学期望.
设 的内角
的内角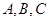 所对的边分别为
所对的边分别为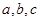 ,且有
,且有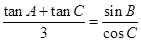 .
.
(1)求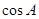 的值;
的值;
(2)若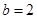 ,
, ,
, 为
为 上一点.且
上一点.且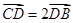 ,求
,求 的长.
的长.
过双曲线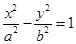
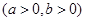 的左焦点
的左焦点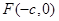
 ,作倾斜角为
,作倾斜角为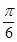 的直线
的直线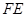 交该双曲线右支于点
交该双曲线右支于点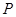 ,若
,若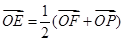 ,且
,且 ,则双曲线的离心率为__________.
,则双曲线的离心率为__________.
已知函数f(x)=lnx-a2x2+ax(a R).
R).
(l)当a=1时,证明:函数f(x)只有一个零点;
(2)若函数f(x)在区间(1,十 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.