(本小题满分14分)
已知函数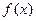 对一切实数x,y都有
对一切实数x,y都有 成立,且
成立,且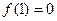 .
.
(1)求 的值
的值
(2)求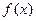 的解析式
的解析式
(3)若 ,对任意的
,对任意的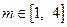 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围
(本小题满分14分)
已知等差数列 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,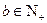 ,且
,且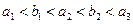 .
.
(Ⅰ)a的值;
(Ⅱ) 若对于任意 ,总存在
,总存在 ,使
,使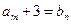 ,求b的值;
,求b的值;
(Ⅲ) 在(Ⅱ)中,记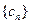 是所有
是所有 中满足
中满足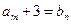 ,
, 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记 为
为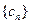 的前n项和,
的前n项和, 是
是 的前n项和,求证:
的前n项和,求证: ≥
≥
 .
.
已知椭圆G的中心在坐标原点,与双曲线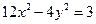 有相同的焦点,且过点
有相同的焦点,且过点 .
.
(Ⅰ) 求椭圆G的方程;
(Ⅱ) 设 、
、 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过 的直线
的直线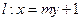 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
(本小题满分14分)
如图6,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,EF⊥PB交PB于点F.
(Ⅰ) 若PD=DC=2求三棱锥A-BDE的体积;
(Ⅱ) 证明PA∥平面EDB;
(Ⅲ) 证明PB⊥平面EFD.
(本小题满分12分)
某单位组织50名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,创导文明新风;2、到指定的社区、车站、码头做义工,帮助那些需要帮助的人。各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| 宣传慰问 |
义工救助 |
总计 |
|
| 20至40岁 |
11 |
16 |
27 |
| 大于40岁 |
15 |
8 |
23 |
| 总计 |
26 |
24 |
50 |
(Ⅰ) 用分层抽样方法在做义工的志愿者中随机抽取6名,大于40岁的应该抽取几名?
(Ⅱ) 在上述抽取的6名志愿者中任取2名,求恰有1名志愿者年龄大于40岁的概率.
(Ⅲ)如果“宣传慰问”与“做义工”是两个分类变量,并且计算出随机变量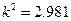 ,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
(本小题满分14分)
在DABC中,角A、B、C所对的边分别为a、b、c,若 ,
, ,
, .
.
(I) 求c的值; (II) 求 的值.
的值.