(本小题满分12分)如图, 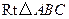 内接于
内接于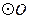 ,
,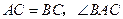 的平分线
的平分线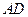 与
与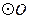 交于点
交于点 ,与
,与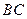 交于点
交于点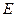 ,延长
,延长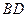 ,与
,与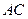 的延长线交于点
的延长线交于点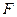 ,连接
,连接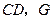 是
是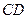 的中点,连结
的中点,连结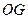 .
.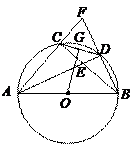
(1)判断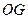 与
与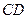 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;
(2)求证: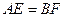 ;
;
(3)若 ,求
,求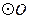 的面积.
的面积.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.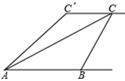
(1)求气球的高度(结果精确到0.1米);
(2)求气球飘移的平均速度(结果保留3个有效数字).
如图,AD∥BC,∠A=90°,以点B为圆心,BC长为半径画弧,交射线AD于点E,连接BE,过点C作CF⊥BE,垂足为F,求证:AB=FC.
甲、乙、丙三位同学用质地大小完全一样的纸片分别制作一张卡片a、b、c,收集后放在一个不透明的箱子中,然后每人从箱子中随机抽取一张.
(1)用列表或画树状图的方法表示三位同学抽到卡片的所有可能的结果;
(2)求三位同学中至少有一人抽到自己制作卡片的概率.
本区某校对学生开展“不闯红灯,珍爱生命”的教育,为此校学生会委员在某天到市中心某十字路口,观察、统计上午7∶00~12∶00之间闯红灯的人次,制作了如下两个统计图:
(1)图一中各时段闯红灯人次的平均数为人次,中位数是人次;
(2)该路口这一天上午7∶00~12∶00闯红灯的未成年人有人次;
(3)估计一周(七天)内该路口上午7∶00~12∶00闯红灯的中青年约有人次;
(4)是否能以此估计全市这一天上午7∶00~12∶00所有路口闯红灯的人次?为什么?
(1)解方程: ;(2)化简:
;(2)化简: