如图,AD∥BC,∠A=90°,以点B为圆心,BC长为半径画弧,交射线AD于点E,连接BE,过点C作CF⊥BE,垂足为F,求证:AB=FC.
如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移2格.请在图中画出平移后的△A′B′C′,并作出△A′B′C′边A′B′上的高A′D′,再写出图中与线段AC平行的线段。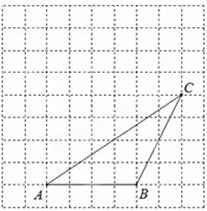
(1)若26=a2=4b(a>0),求a+b值。 (2)若3x=2,3y=4,求92x-y+27x-y的值。
先化简,再求值: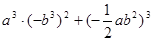 ,其中
,其中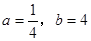 。
。
计算:(每小题5分,共20分)
(1) 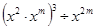 ;(2)
;(2)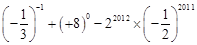 ;
;
(3)  ; (4)
; (4)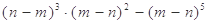
小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤。
妈妈:“今天买这两样菜共花了45元,上月买同样重量的这两种菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨了50%,排骨的单价上涨了20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你根据上述信息,通过列方程组替小明求解这天萝卜、排骨的单价(单位:元/斤)。