(本小题满分12分)已知:抛物线 的对称轴为
的对称轴为 与
与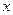 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 其中
其中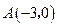 、
、

(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得 的周长最小.请求出点P的坐标.
的周长最小.请求出点P的坐标.
(3)若点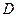 是线段
是线段 上的一个动点(不与点O、点C重合).过点D作
上的一个动点(不与点O、点C重合).过点D作 交
交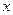 轴于点
轴于点 连接
连接 、
、 .设
.设 的长为
的长为 ,
, 的面积为
的面积为 .求
.求 与
与 之间的函数关系式.试说明
之间的函数关系式.试说明 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
(1)解方程:x2+4x-1=0
(2)解不等式组: .
.
如图,在平面直角坐标系中,直线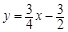 与抛物线
与抛物线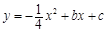 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.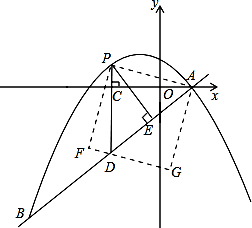
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为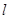 ,点P的横坐标为
,点P的横坐标为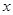 ,求
,求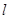 关于
关于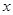 的函数关系式,并求出
的函数关系式,并求出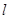 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
如图,在平面直角坐标系中,直线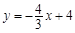 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.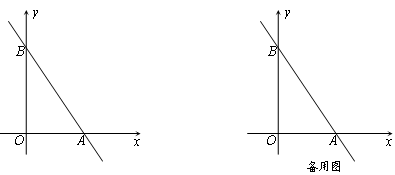
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值.
某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
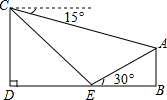
如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: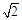 ≈1.41).
≈1.41).