如图，在平面直角坐标系中，直线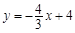分别交x轴、y轴于A、B两点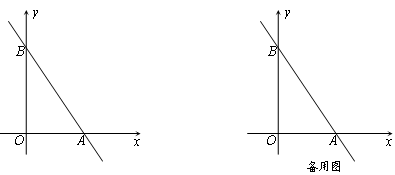．-优题课

如图，在平面直角坐标系中，直线分别交x轴、y轴于A、B两点．

（1）求A、B两点的坐标；
（2）设P是直线AB上一动点（点P与点A不重合），⊙P始终和x轴相切，和直线AB相交于C、D两点（点C的横坐标小于点D的横坐标）．若P点的横坐标为m，试用含有m的代数式表示点C的横坐标；
（3）在（2）的条件下，若点C在线段AB上，当△BOC为等腰三角形时求m的值．

科目数学题型解答题难度中等

知识点：一次函数的最值

先化简，再从 $- 1$ ，0，1，2， $\sqrt{2} + 1$ 中选择一个合适的 $x$ 的值代入求值． $(1 - \frac{x}{x + 1}) \div \frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ．

计算： ${(2021 - π)}^{0} - | \sqrt{3} - 2 | - \tan 60 °$ ．

如图，在直角坐标系中，二次函数 $y = x^{2} + bx + c$ 的图象与 $x$ 轴相交于点 $A (- 1, 0)$ 和点 $B (3, 0)$ ，与 $y$ 轴交于点 $C$ ．

（1）求 $b$ 、 $c$ 的值；

（2）点 $P (m, n)$ 为抛物线上的动点，过 $P$ 作 $x$ 轴的垂线交直线 $l : y = x$ 于点 $Q$ ．

①当 $0 < m < 3$ 时，求当 $P$ 点到直线 $l : y = x$ 的距离最大时 $m$ 的值；

②是否存在 $m$ ，使得以点 $O$ 、 $C$ 、 $P$ 、 $Q$ 为顶点的四边形是菱形，若不存在，请说明理由；若存在，请求出 $m$ 的值．

如图①， $E$ 、 $F$ 是等腰 $Rt Δ ABC$ 的斜边 $BC$ 上的两动点， $∠ EAF = 45 °$ ， $CD ⊥ BC$ 且 $CD = BE$ ．

（1）求证： $ΔABE ≅ ΔACD$ ；

（2）求证： $E F^{2} = B E^{2} + C F^{2}$ ；

（3）如图②，作 $AH ⊥ BC$ ，垂足为 $H$ ，设 $∠ EAH = α$ ， $∠ FAH = β$ ，不妨设 $AB = \sqrt{2}$ ，请利用（2）的结论证明：当 $α + β = 45 °$ 时， $\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$ 成立．

如图，点 $A$ 在以 $BC$ 为直径的 $⊙ O$ 上， $∠ ABC$ 的角平分线与 $AC$ 相交于点 $E$ ，与 $⊙ O$ 相交于点 $D$ ，延长 $CA$ 至 $M$ ，连结 $BM$ ，使得 $MB = ME$ ，过点 $A$ 作 $BM$ 的平行线与 $CD$ 的延长线交于点 $N$ ．

（1）求证： $BM$ 与 $⊙ O$ 相切；

（2）试给出 $AC$ 、 $AD$ 、 $CN$ 之间的数量关系，并予以证明．

试卷网试题网古诗词网作文网范文网