((本题13分)汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为 ,写出
,写出 关于
关于 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
(本小题满分15分)如图,已知 平面
平面 ,
, ,
, ,
, ,
,
为等边三角形.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分15分)已知数列 满足
满足 ,
, .令
.令 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)求证: .
.
(本小题满分15分)已知在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,且满足
的对边,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若点 为边
为边 的中点,求
的中点,求 面积的最大值.
面积的最大值.
(本小题满分14分)已知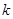 为实数,对于实数
为实数,对于实数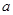 和
和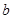 ,定义运算“
,定义运算“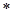 ”:
”: 
设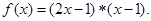
(1)若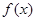 在
在 上为增函数,求实数
上为增函数,求实数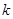 的取值范围;
的取值范围;
(2)已知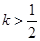 ,且当
,且当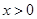 时,
时, 恒成立,求
恒成立,求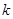 的取值范围.
的取值范围.
(本小题满分15分)如果数列 同时满足以下两个条件:(1)各项均不为0;(2)存在常数
同时满足以下两个条件:(1)各项均不为0;(2)存在常数 ,
,
对任意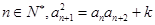 都成立,则称这样的数列
都成立,则称这样的数列 为“
为“ 类等比数列”.
类等比数列”.
(Ⅰ)若数列 满足
满足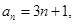 证明数列
证明数列 为“
为“ 类等比数列”,并求出相应的
类等比数列”,并求出相应的 的值;
的值;
(Ⅱ)若数列 为“
为“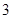 类等比数列”,且满足
类等比数列”,且满足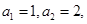 问是否存在常数
问是否存在常数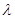 ,使得
,使得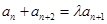 对
对
任意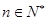 都成立?若存在,求出
都成立?若存在,求出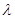 ,若不存在,请举出反例.
,若不存在,请举出反例.