(本小题满分14分)已知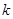 为实数,对于实数
为实数,对于实数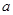 和
和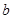 ,定义运算“
,定义运算“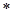 ”:
”: 
设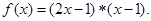
(1)若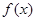 在
在 上为增函数,求实数
上为增函数,求实数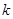 的取值范围;
的取值范围;
(2)已知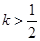 ,且当
,且当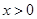 时,
时, 恒成立,求
恒成立,求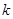 的取值范围.
的取值范围.
(本小题满分12分)如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为α,再由点C沿东偏北β(β<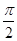 )角方向走d米到达位置D,测得∠BDC=γ.
)角方向走d米到达位置D,测得∠BDC=γ.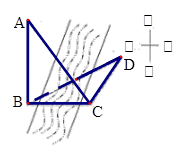
(Ⅰ)若β=75°,求sⅠn∠BCD的值;
(Ⅱ)求此建筑物的高度(用字母表示).
(本小题满分14分)已知函数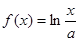 .
.
(1)若曲线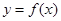 在
在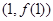 处的切线为
处的切线为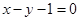 ,求
,求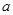 的值;
的值;
(2)设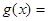
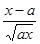 ,
,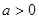 ,证明:当
,证明:当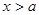 时,
时,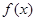 的图象始终在
的图象始终在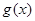 的图象的下方;
的图象的下方;
(3)当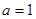 时,设
时,设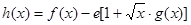 ,(
,(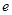 为自然对数的底数),
为自然对数的底数),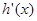 表示
表示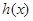 导函数,求证:对于曲线
导函数,求证:对于曲线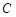 上的不同两点
上的不同两点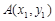 ,
,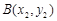 ,
,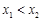 ,存在唯一的
,存在唯一的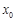
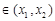 ,使直线
,使直线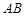 的斜率等于
的斜率等于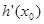 .
.
(本小题满分14分)根据如图所示的程序框图,将输出a,b的值依次分别记为a1,a2, ,an, ,a2008;b1,b2, ,bn, ,b2008.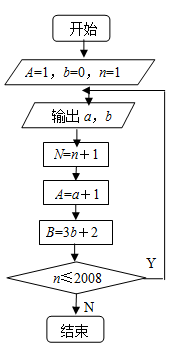
(Ⅰ)求数列 { an } 的通项公式;
(Ⅱ)写出b1,b2,b3,b4,由此猜想{ bn }的通项公式,并证明你的证明;
(Ⅲ)在 ak 与 ak+1 中插入bk+1个3得到一个新数列 { cn } ,设数列 { cn }的前n项和为Sn,问是否存在这样的正整数m,使数列{ cn }的前m项的和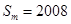 ,如果存在,求出m的值,如果不存在,请说明理由.
,如果存在,求出m的值,如果不存在,请说明理由.
已知椭圆 的离心率为
的离心率为 ,其左右焦点分别为
,其左右焦点分别为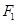 、
、 ,
, ,设点
,设点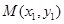 ,
,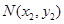 是椭圆上不同两点,且这两点与坐标原点的连线的斜率之积
是椭圆上不同两点,且这两点与坐标原点的连线的斜率之积 .(1)求椭圆
.(1)求椭圆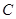 的方程;(2)求证:
的方程;(2)求证: 为定值,并求该定值.
为定值,并求该定值.
(本小题满分14分)在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边 列联表,并判断是否有
列联表,并判断是否有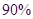 的把握认为“测评结果优秀与性别有关”.
的把握认为“测评结果优秀与性别有关”.
| 男生 |
女生 |
总计 |
|
| 优秀 |
|||
| 非优秀 |
|||
| 总计 |
参考数据与公式: ,其中
,其中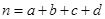 .
.
临界值表:
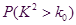 |
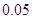 |
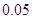 |
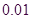 |
 |
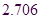 |
 |
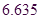 |