已知数列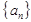
的前
项和为
，
，
是
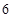与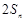
的等差中项（
）.
（Ⅰ）证明数列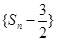
为等比数列；
（Ⅱ）求数列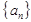的通项公式；
（Ⅲ）是否存在正整数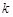
，使不等式
（）恒成立，若存在，求出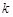的最大值；若不存在，请说明理由.
（本小题满分14分）
已知函数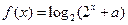
（a为常数）是R上的奇函数，函数
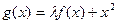是区间[-1，1]上的减函数.
（I）求a的值；
（II）若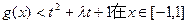
上恒成立，求t的取值范围；
（III）讨论关于x的方程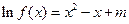
解的情况，并求出相应的m的取值范围.
（本小题满分13分）
如图，ABCD是块矩形硬纸板，其中AB=2AD= 2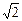
，E为DC中点，将它沿AE折成直二面角D-AE-B.
（Ⅰ）求证：AD⊥平面BDE；
（Ⅱ）求二面角B-AD-E的余弦值.
（本小题满分13分）
某班从6名班干部（其中男生4人，女生2人）中选3人参加学校学生会的干部竞选．
（Ⅰ）设所选3人中女生人数为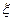
，求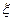的分布列及数学期望
；
（Ⅱ）在男生甲被选中的情况下，求女生乙也被选中的概率．
已知函数f (x) = 2cos2x-2sinxcosx + 1．
（1）设方程f (x) – 1 = 0在(0，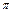
)内的
两个零点x1，x2，求x1 + x2的值；
（2）把函数y = f (x)的图象
向左平移m (m＞0)个单位使所得函数的图象关于点(0，2)对称，求m的最小值．
(本小题满分14分)
已知函数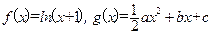
.
（1）若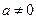
，曲线
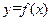和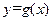
在原点处的切线重合，求实数
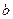的值.
（2）若
，
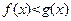在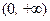
上恒成立，求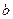的取值范围.
（3）函数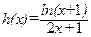
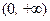，在上函数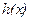
图象与直线y=1是否有交点？若有，求出交点，若没有，请说明理由.