(本小题满分15分)如果数列 同时满足以下两个条件:(1)各项均不为0;(2)存在常数
同时满足以下两个条件:(1)各项均不为0;(2)存在常数 ,
,
对任意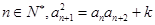 都成立,则称这样的数列
都成立,则称这样的数列 为“
为“ 类等比数列”.
类等比数列”.
(Ⅰ)若数列 满足
满足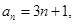 证明数列
证明数列 为“
为“ 类等比数列”,并求出相应的
类等比数列”,并求出相应的 的值;
的值;
(Ⅱ)若数列 为“
为“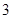 类等比数列”,且满足
类等比数列”,且满足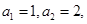 问是否存在常数
问是否存在常数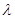 ,使得
,使得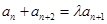 对
对
任意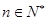 都成立?若存在,求出
都成立?若存在,求出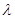 ,若不存在,请举出反例.
,若不存在,请举出反例.
如图,正三棱柱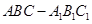 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是 棱的中点,AE交
棱的中点,AE交 于点H.
于点H.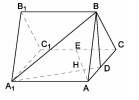
(1)求证: 平面
平面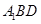 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点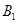 到平面
到平面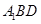 的距离.
的距离.
已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点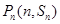 都在函数
都在函数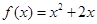 的图像上,且过点
的图像上,且过点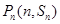 的切线的斜率为
的切线的斜率为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设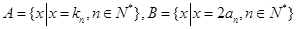 ,等差数列
,等差数列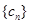 的任一项
的任一项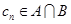 ,其中
,其中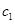 是
是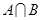 中所有元素的最小数,
中所有元素的最小数,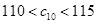 ,求
,求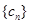 的通项公式.
的通项公式.
2014年2月21日,《中共中央关于全面深化改革若干重大问题的决定》明确:坚持计划生育的基本国策,启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法,某媒体在该地区选择了3600人调查,就是否赞成“单独两孩”的问题,调查统计的结果如下表:
 |
赞成 |
反对 |
无所谓 |
| 农村居民 |
2100人 |
120人 |
y人 |
| 城镇居民 |
600人 |
x人 |
z人 |
已知在全体样本中随机抽取1人,抽到持“反对”态度的人的概率为0.05.
(1)现在分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,按每组3人分成两组进行深入交流,求第一组中农村居民人数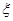 的分布列和数学期望.
的分布列和数学期望.
设 函数
函数 满足
满足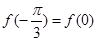 .
.
(1)求 的单调递减区间;
的单调递减区间;
(2)设锐角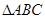 的内角
的内角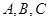 所对的边分别为
所对的边分别为 ,且
,且 ,求
,求 的取值范围.
的取值范围.
已知函数
(1)判断函数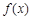 的奇偶性;
的奇偶性;
(2)试用函数单调性定义说明函数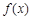 在区间
在区间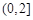 和
和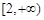 上的增减性;
上的增减性;
(3)若 满足:
满足: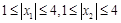 ,试证明:
,试证明: .
.