已知椭圆的中心为原点 ,长轴在 轴上,上顶点为 ,左、右焦点分别为 ,线段 的中点分别为 ,且 是面积为4的直角三角形.

(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过
作直线
交椭圆于
,
,求直线
的方程
【2015高考广东,理17】某工厂36名工人的年龄数据如下表:
| 工人编号 |
年龄 |
工人编号 |
年龄 |
工人编号 |
年龄 |
工人编号 |
年龄 |
| 1 |
40 |
10 |
36 |
19 |
27 |
28 |
34 |
| 2 |
44 |
11 |
31 |
20 |
43 |
29 |
39 |
| 3 |
40 |
12 |
38 |
21 |
41 |
30 |
43 |
| 4 |
41 |
13 |
39 |
22 |
37 |
31 |
38 |
| 5 |
33 |
14 |
43 |
23 |
34 |
32 |
42 |
| 6 |
40 |
15 |
45 |
24 |
42 |
33 |
53 |
| 7 |
45 |
16 |
39 |
25 |
37 |
34 |
37 |
| 8 |
42 |
17 |
38 |
26 |
44 |
35 |
49 |
| 9 |
43 |
18 |
36 |
27 |
42 |
36 |
39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的平均值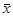 和方差
和方差 ;
;
(3)36名工人中年龄在 与
与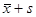 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?
【2015高考北京,理16】 ,
,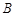 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下: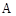 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,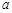
假设所有病人的康复时间互相独立,从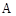 ,
, 两组随机各选1人,
两组随机各选1人,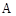 组选出的人记为甲,
组选出的人记为甲, 组选出的人记为乙.
组选出的人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果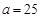 ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当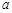 为何值时,
为何值时,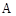 ,
, 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)
【2015高考新课标1,理19】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费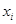 和年销售量
和年销售量 (
( =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.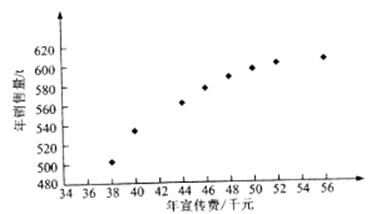
  |
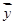 |
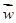 |
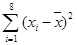 |
 |
 |
 |
| 46.6 |
56.3 |
6.8 |
289.8 |
1.6 |
1469 |
108.8 |
表中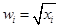 ,
,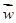 =
=
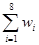
(Ⅰ)根据散点图判断,y=a+bx与y=c+d 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据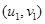 ,
,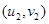 ,……,
,……, ,其回归线
,其回归线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: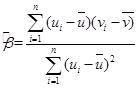 ,
,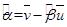
【2015高考陕西,理19】(本小题满分12分)设某校新、老校区之间开车单程所需时间为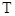 ,
,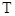 只与道路畅通状况有关,对其
只与道路畅通状况有关,对其
容量为 的样本进行统计,结果如下:
的样本进行统计,结果如下:
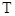 (分钟) (分钟) |
25 |
30 |
35 |
40 |
| 频数(次) |
20 |
30 |
40 |
10 |
(Ⅰ)求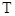 的分布列与数学期望
的分布列与数学期望 ;
;
(Ⅱ)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授
从离开老校区到返回老校区共用时间不超过120分钟的概率.
【2015高考湖北,理20】某厂用鲜牛奶在某台设备上生产 两种奶制品.生产1吨
两种奶制品.生产1吨 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨
产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天
产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天 产品的产量不超过
产品的产量不超过 产品产量的2倍,设备每天生产
产品产量的2倍,设备每天生产 两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
| W |
12 |
15 |
18 |
| P |
0.3 |
0.5 |
0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利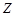 (单位:元)是一个随机变量.
(单位:元)是一个随机变量.
(Ⅰ)求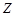 的分布列和均值;
的分布列和均值;
(Ⅱ)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.