意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序.
怀化市某棚户区改造工程规划用地近似为图中半径为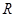 的圆面,图中圆内接四边形
的圆面,图中圆内接四边形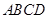 为拟定拆迁的棚户区,测得
为拟定拆迁的棚户区,测得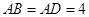 百米,
百米, 百米,
百米,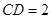 百米.
百米.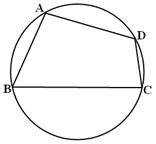
(Ⅰ)请计算原棚户区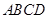 的面积及圆面的半径
的面积及圆面的半径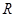 ;
;
(Ⅱ)因地理条件的限制,边界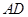 ,
,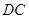 不能变更,而边界
不能变更,而边界 ,
,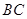 可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧 上求出一点
上求出一点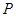 ,使得棚户区改造的新建筑用地
,使得棚户区改造的新建筑用地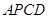 的面积最大,并求最大值.
的面积最大,并求最大值.
如图,四面体 中,
中, 、
、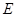 分别是
分别是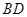 、
、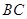 的中点,
的中点,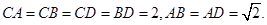
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求异面直线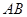 与
与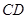 所成角余弦值的大小;
所成角余弦值的大小;
(Ⅲ)求点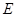 到平面
到平面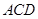 的距离.
的距离.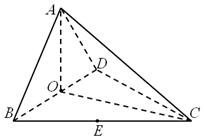
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示。
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
[160,165) |
5 |
0.05 |
| 第二组 |
[165,170) |
35 |
0.35 |
| 第三组 |
[170,175) |
30 |
a |
| 第四组 |
[175,180) |
b |
0.2 |
| 第五组 |
[180,185) |
10 |
0.1 |
(Ⅰ)求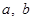 的值;
的值;
(Ⅱ)为了能选出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12人进入第二轮面试,求第3、4、5组中每组各抽取多少人进入第二轮的面试;考生李翔的笔试成绩为178分,但不幸没入选这100人中,那这样的筛选方法对该生而言公平吗?为什么?
(Ⅲ)在(2)的前提下,学校决定在12人中随机抽取3人接受“王教授”的面试,设第4组中被抽取参加“王教授”面试的人数为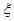 ,求
,求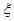 的分布列和数学期望.
的分布列和数学期望.
已知函数
(Ⅰ)求函数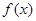 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)设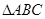 的内角
的内角 、
、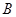 、
、 的对边分别为
的对边分别为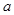 、
、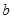 、
、 且
且 ,
,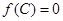 ,若向量
,若向量 与向量
与向量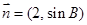 共线,求
共线,求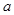 、
、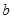 的值.
的值.
已知函数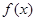 的定义域是
的定义域是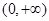 ,
,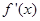 是
是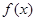 的导函数,且
的导函数,且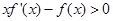 在
在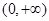 内恒成立.
内恒成立.
求函数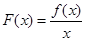 的单调区间;
的单调区间;
若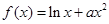 ,求
,求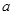 的取值范围;
的取值范围;
(3)设 是
是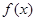 的零点,
的零点,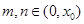 ,求证:
,求证: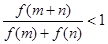 .
.