某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示。
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
[160,165) |
5 |
0.05 |
| 第二组 |
[165,170) |
35 |
0.35 |
| 第三组 |
[170,175) |
30 |
a |
| 第四组 |
[175,180) |
b |
0.2 |
| 第五组 |
[180,185) |
10 |
0.1 |
(Ⅰ)求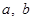 的值;
的值;
(Ⅱ)为了能选出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12人进入第二轮面试,求第3、4、5组中每组各抽取多少人进入第二轮的面试;考生李翔的笔试成绩为178分,但不幸没入选这100人中,那这样的筛选方法对该生而言公平吗?为什么?
(Ⅲ)在(2)的前提下,学校决定在12人中随机抽取3人接受“王教授”的面试,设第4组中被抽取参加“王教授”面试的人数为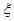 ,求
,求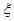 的分布列和数学期望.
的分布列和数学期望.
已知动点 到直线
到直线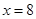 的距离是它到点
的距离是它到点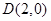 的距离的2倍.记
的距离的2倍.记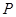 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)求定圆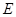 的方程,使圆
的方程,使圆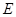 与以
与以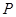 为圆心,
为圆心,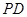 为半径的圆内切.
为半径的圆内切.
(3)已知定点 ,是否存在斜率为1的直线
,是否存在斜率为1的直线 与曲线
与曲线 交于不同的两点
交于不同的两点 ,使得
,使得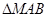 是以
是以 为底边为等腰三角形,若存在,求出
为底边为等腰三角形,若存在,求出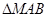 的面积,若不存在,说明理由.
的面积,若不存在,说明理由.
为了减少放射性污染对人体的影响,某市环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻
与时刻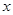 (时)的关系为
(时)的关系为 ,其中
,其中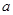 是与气象有关的参数,且
是与气象有关的参数,且 ,若用每天
,若用每天 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作 .
.
(1)令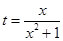 ,
,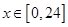 ,求
,求 的取值范围;
的取值范围;
(2)国家环保局规定,每天的综合放射性污染指数不得超过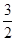 ,试问目前市中心的综合放射性污染指数是否超标?
,试问目前市中心的综合放射性污染指数是否超标?
(本小题满分14分)如图,三棱柱 的体积为1,
的体积为1,
(1)若 ,
,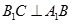 ,证明:平面
,证明:平面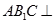 平面
平面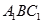 ;
;
(2)设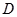 是边
是边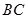 上的一点(不含
上的一点(不含 点),
点), ,
,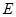 在
在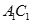 上,且
上,且 平面
平面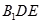 ,求三棱锥
,求三棱锥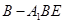 的体积,并求出三棱锥
的体积,并求出三棱锥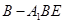 体积的最大值.
体积的最大值.
在 中,角
中,角 所对边分别为
所对边分别为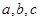 ,且向量
,且向量 ,
, ,满足
,满足 .
.
(1)求角C的大小;
(2)若 ,求
,求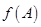 的取值范围.
的取值范围.
已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|-2≤x≤1}.
(1)求a的值,
(2)若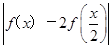 ≤k恒成立,求k的取值范围.
≤k恒成立,求k的取值范围.