已知函数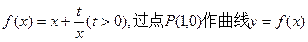 的两条切线PM、PN,切点分别为M、N.
的两条切线PM、PN,切点分别为M、N.
(I)当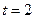 时,求函数
时,求函数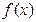 的单调递增区间;
的单调递增区间;
(II)设|MN|=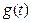 ,试求函数
,试求函数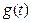 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数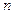 ,在区间
,在区间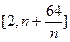 内,总存在m+1个数
内,总存在m+1个数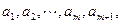 使得不等式
使得不等式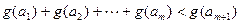 成立,求m的最大值.
成立,求m的最大值.
已知 各项均为正数的数列
各项均为正数的数列 满足
满足 ,
, ,
,  .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)当 取何值时,
取何值时, 取最大值,并求出最大值;
取最大值,并求出最大值;
(Ⅲ)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
1已知函数 ,且
,且 ,
, .
.
(Ⅰ)求 的值域
的值域
(Ⅱ)指出函数 的单调性(不需证明),并求解关于实数
的单调性(不需证明),并求解关于实数 的不等式
的不等式 ;
;
(Ⅲ)定义在 上的函数
上的函数 满足
满足 ,且当
,且当 时
时 求方程
求方程 在区间
在区间 上的解的个数.
上的解的个数.
设 ,
, ,Q=
,Q= ;若将
;若将 ,
, ,
, 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列 的前三项
的前三项 (I)在使得
(I)在使得 ,
, ,
, 有意义的条件下,试比较
有意义的条件下,试比较 的大小;
的大小;
(II)求 的值及数列
的值及数列 的通项;
的通项;
(III)记函数 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为 ,设
,设 ,求
,求 .
.
设函数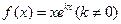
(1)求曲线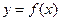 在点
在点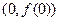 处的切线方程;
处的切线方程;
(2)求函数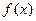 的单调区间;
的单调区间;
(3)若函数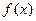 在区间
在区间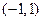 内单调递增,求
内单调递增,求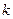 的取值范围.
的取值范围.
已知函数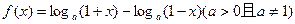
(1)讨论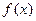 的奇偶性与单调性;
的奇偶性与单调性;
(2)若不等式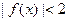 的解集为
的解集为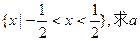 的值;
的值;
(3)(文)设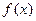 的反函数为
的反函数为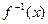 ,若关于
,若关于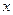 的不等式
的不等式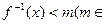 R)有解,求
R)有解,求 的取值范围.
的取值范围.
(理)设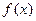 的反函数为
的反函数为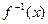 ,若
,若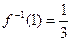 ,解关于
,解关于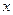 的不等式
的不等式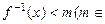 R).
R).