如图，某市有一块长为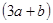
米，宽为
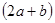米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当
，
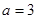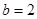时的绿化面积．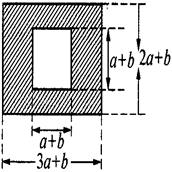
如图，D、E分别是AC、AB上的点，∠ADE=40°，∠C=40°，∠AED=80°
（1）DE与BC平行吗？请说明理由；
（2）求∠B的度数。
解下列方程组
（1）
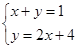（2）
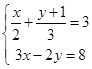
去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．
（1）求饮用水和蔬菜各有多少件？
现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；
（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？
阅读下列解方程组的方法，回答问题．解方程组
解：由①﹣②得2x+2y=2即x+y=1
③×16得16x+16y=16④
②﹣④得x=﹣1，从而可得y=2∴原方程组的解是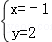
．
（1）请你仿上面的解法解方程组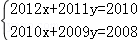
；
（2）请大胆猜测关于x、y的方程组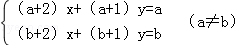
的解是什么？
（2） 