(满分l2分)学完“等边三角形”这一节后,老师布置了一道思考题:
如图,点M,N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.
求证:∠BQM=60°.
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC,CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?
请你作出判断,在下列横线上填写“是”或“否”:①______;②______;③______.并对②,③的判断,选择一个给出证明.
新华商场销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
. 如图,已知点E是矩形ABCD的边CD上一点,BF⊥AE于点F,
求证:△ABF∽△EAD.
辨析纠错.
已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.对于这道题,
小明是这样证明的.
证明:∵AD平分∠BAC,∴∠1=∠2(角平分线的定义).
∵DE∥AC,∴∠2=∠3(两直线平行,内错角相等).
∴∠1=∠3(等量代换).
∴AE=DE(等角对等边).同理可证:AF=DF.
∴ 四边形AEDF是菱形(菱形定义).
老师说小明的证明过程有错误,你能看出来吗?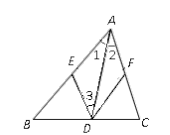
(1)请你帮小明指出他错在哪里.
(2)请你帮小明做出正确的解答.
如下图,路灯下,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN。
(1)试确定路灯的位置(用点P表示)。
(2)在图中画出表示大树高的线段。
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树。
画出下面实物的三视图: