(满分l0分)如图,A,B两点分别位于一个池塘的两端,由于受条件限制无法直接度量A,B间的距离.小明利用学过的知识,设计了如下三种测量方法,如图①,②,③所示(图中a,b,c…表示长度,α,β,θ…表示角度).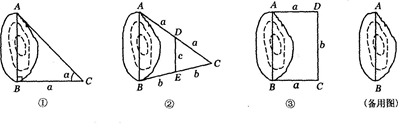
(1)请你写出小明设计的三种测量方法中AB的长度:图①AB=_______,图②AB=_______,图③AB=_______;
(2)请你再设计一种不同于以上三种的测量方法,画出示意图(不要求写画法),用字母标注需测量的边或角,并写出AB的长度.
菱形 的对角线 , 相交于点 , ,点 是射线 上一个动点,过点 作 交射线 于点 ,以 , 为邻边作矩形 .
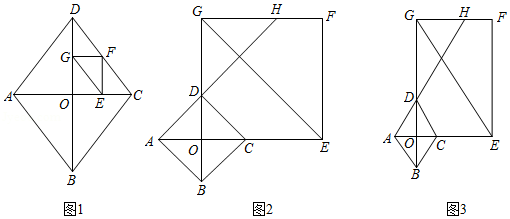
(1)如图1,当点 在线段 上时,求证: ;
(2)若延长 与边 交于点 ,将 沿直线 翻折 得到 .
①如图2,当点 在 上时,求证:四边形 为正方形;
②如图3,当 为定值 时,设 , 为大于0的常数,当且仅当 时,点 在矩形 的外部,求 的值.
资料:公司营销区域面积是指公司营销活动范围内的地方面积,公共营销区域面积是指两家及以上公司营销活动重叠范围内的地方面积.
材料:某地有 , 两家商贸公司(以下简称 , 公司).去年下半年 , 公司营销区域面积分别为 平方千米, 平方千米,其中 ,公共营销区域面积与 公司营销区域面积的比为 ;今年上半年,受政策鼓励,各公司决策调整, 公司营销区域面积比去年下半年增长了 , 公司营销区域面积比去年下半年增长的百分数是 公司的4倍,公共营销区域面积与 公司营销区域面积的比为 ,同时公共营销区域面积与 , 两公司总营销区域面积的比比去年下半年增加了 个百分点.
问题:
(1)根据上述材料,针对去年下半年,提出一个你喜欢的数学问题(如求去年下半年公共营销区域面积与 公司营销区域面积的比),并答案;
(2)若同一个公司去年下半年和今年上半年每平方千米产生的经济收益持平,且 公司每半年每平方千米产生的经济收益均为 公司的1.5倍,求去年下半年与今年上半年两公司总经济收益之比.
如图,在四边形 中, , , ,过点 的 与边 , 分别交于 , 两点. ,垂足为 , .连接 , , .

(1)若 ,试判断 的形状,并说明理由;
(2)若 ,求证: 与 相切于点 .
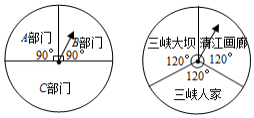
宜昌景色宜人,其中三峡大坝、清江画廊、三峡人家景点的景色更是美不胜收.某民营单位为兼顾生产和业余生活,决定在下设的 , , 三部门利用转盘游戏确定参观的景点.两转盘各部分圆心角大小以及选派部门、旅游景点等信息如图.
(1)若规定老同志相对偏多的部门选中的可能性大,试判断这个部门是哪个部门?请说明理由;
(2)设选中 部门游三峡大坝的概率为 ,选中 部门游清江画廊或者三峡人家的概率为 ,请判断 , 大小关系,并说明理由.
红光中学学生乘汽车从学校去研学旅行基地,以75千米 小时的平均速度,用时2小时到达.由于天气原因,原路返回时汽车平均速度控制在不低于50千米 小时且不高于60千米 小时的范围内,这样需要用 小时到达.求 的取值范围.