(每小题8分,共16分)
(1)先化简: ,然后从
,然后从 ,1,-1中选取一个能使结果为整数的数作为x的值代入求值.
,1,-1中选取一个能使结果为整数的数作为x的值代入求值.
(2)面对全球金融危机的挑战,我国政府毅然启动拉动内需的政策,改善民生.国务院决定从2009年2月1日起,“家电下乡”在全国范围内实施,农民购买入选产品,政府按原价购买总额的l3%给予补贴返还.某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电,已知购买冰箱的数量是电视机的2倍,且按原价购买冰箱总额为40000元、电视机总额为l5000元.根据“家电下乡”优惠政策,每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元,问:冰箱、电视机各购买多少台?
阳光明媚的一天,郑州某中学数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),可以提供的测量工具:皮尺、标杆、一副三角尺、小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.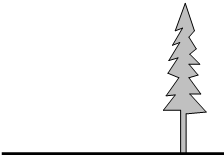
(1)所需的测量工具是:__________;
(2)请画出测量示意图;
(3)设树高为x,请用所测数据(用小写字母表示)求出x.
某气球生产厂家为了确定各种颜色气球的生产比例,确定进行一次调查.如果你是该次调查的负责人,请解决以下问题:
(1)此次调查的对象是什么?适宜采取哪种调查方式?
(2)请设计一个问卷调查表并简要说说你设计的意图.
在学习分式计算时有这样一道题:先化简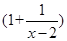 ÷
÷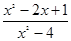 ,再选取一个你喜欢且合适的数代入求值.张明同学化简过程如下:
,再选取一个你喜欢且合适的数代入求值.张明同学化简过程如下:
解: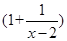 ÷
÷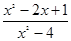
= ÷
÷ ()
()
= ()
()
= ()
()
(1)在括号中直接填入每一步的主要依据或知识点;
(2)如果你是张明同学,那么在选取你喜欢且合适的数进行求值时,你不能选取的数有__________.
小明、小华、小刚三人在一起讨论一个多项式.
小明:它是个三次多项式,且有三项;
小华:其中三次项系数是1;
小刚:在进行分解因式的过程中用到了提公因式法和公式法.
请你试着写出符合上述条件的多项式,并将这个多项式分解因式.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,B、C、G三点在一条直线上,且边长分别为2和3,在BG上截取GP=2,连结AP、PF.
(1)观察猜想AP与PF之间的大小关系,并说明理由;
(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由;
(3)若把这个图形沿着PA、PF剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.