选修4-1:几何证明选讲
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,直线OB交于⊙O于点E,D,连接EC,CD。
(1)试判断直线AB与⊙O的位置关系,并加以证明;
(2)若 ,⊙O的半径为3,求OA的长。
,⊙O的半径为3,求OA的长。
已知函数 ,其中a为常数,且
,其中a为常数,且
(1)若 是奇函数,求a的取值集合A;
是奇函数,求a的取值集合A;
(2)当a=-1时,设 的反函数为
的反函数为 ,且函数
,且函数 的图像与
的图像与 的图像关于
的图像关于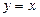 对称,求
对称,求 的取值集合B。
的取值集合B。
(3)对于问题(1)(2)中的A、B,当 时,不等式
时,不等式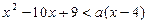 恒成立,求x的取值范围。
恒成立,求x的取值范围。
数列 满足
满足 ,
, .
.
(1)求 通项公式
通项公式 ;
;
(2)令 ,数列
,数列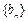 前
前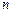 项和为
项和为 ,
,
求证:当 时,
时, ;
;
(3)证明: .
.
已知数列 中,
中, ,对于任意的
,对于任意的 ,有
,有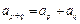
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足:
满足: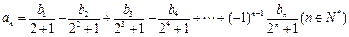 求数列
求数列 的通项公式;
的通项公式;
(3)设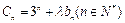 ,是否存在实数
,是否存在实数 ,当
,当 时,
时,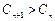 恒成立,若存在,求实数
恒成立,若存在,求实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
已知 各项均为正数的数列
各项均为正数的数列 满足
满足 ,
, ,
,  .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)当 取何值时,
取何值时, 取最大值,并求出最大值;
取最大值,并求出最大值;
(Ⅲ)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
1已知函数 ,且
,且 ,
, .
.
(Ⅰ)求 的值域
的值域
(Ⅱ)指出函数 的单调性(不需证明),并求解关于实数
的单调性(不需证明),并求解关于实数 的不等式
的不等式 ;
;
(Ⅲ)定义在 上的函数
上的函数 满足
满足 ,且当
,且当 时
时 求方程
求方程 在区间
在区间 上的解的个数.
上的解的个数.