请看下面六张卡片,卡片正面分别写有六个数,背面分别写有六个字母a、h、k、n、s、t、,
| 卡片 |
1 |
2 |
3 |
4 |
5 |
6 |
| 正面 |
-0.5 |
-(+2) |
-(-1) |
0 |
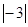 |
 |
| 反面 |
a |
h |
k |
n |
s |
t |
将卡片正面的六个数字在数轴上表示出来;
将卡片正面的数从小到大排列,然后将卡片翻转,看看卡片上的字母组成的是一个什么单词?
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
已知抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.
(1)求抛物线的解析式;
(2)若点D的坐标为(﹣1,0),在直线AB上有一点P,使△ABO与△ADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.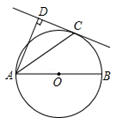
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4,求AC的长.
【原创题】如图:已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=1,AC=2.
求△ECF的面积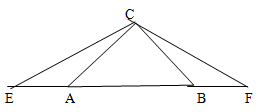
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?