在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD,底面ABCD是菱形,∠A=60°,E是AD的中点,F是PC的中点.
(Ⅰ)求证:BE⊥平面PAD;
( Ⅱ)求证:EF∥平面PAB;
Ⅱ)求证:EF∥平面PAB;
已知椭圆 :
: (
( )过点
)过点 ,且椭圆
,且椭圆 的离心率为
的离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若动点 在直线
在直线 上,过
上,过 作直线交椭圆
作直线交椭圆 于
于 两点,且
两点,且 为线段
为线段 中点,再过
中点,再过 作直线
作直线 .证明:直线
.证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若存在 使不等式
使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,已知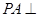 平面
平面 ,四边形
,四边形 是矩形,
是矩形,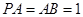 ,
, ,点
,点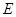 ,
,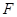 分别是
分别是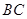 ,
,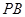 的中点.
的中点.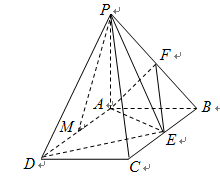
(Ⅰ)求三棱锥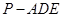 的体积;
的体积;
(Ⅱ)求证: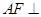 平面
平面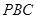 ;
;
(Ⅲ)若点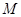 为线段
为线段 中点,求证:
中点,求证: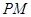 ∥平面
∥平面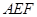 .
.
北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为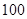 分,规定测试成绩在
分,规定测试成绩在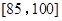 之间为体质优秀;在
之间为体质优秀;在 之间为体质良好;在
之间为体质良好;在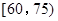 之间为体质合格;在
之间为体质合格;在 之间为体质不合格.
之间为体质不合格.
现从某校高三年级的 名学生中随机抽取
名学生中随机抽取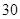 名学生体质健康测试成绩,其茎叶图如下:
名学生体质健康测试成绩,其茎叶图如下: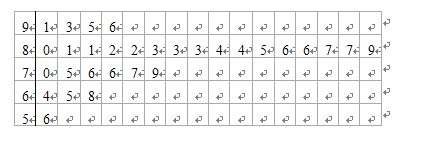
(Ⅰ)试估计该校高三年级体质为优秀的学生人数;
(Ⅱ)根据以上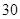 名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取
名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取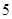 名学生,再从这
名学生,再从这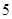 名学生中选出
名学生中选出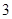 人.
人.
(ⅰ)求在选出的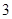 名学生中至少有
名学生中至少有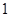 名体质为优秀的概率;
名体质为优秀的概率;
(ⅱ)求选出的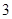 名学生中体质为优秀的人数不少于体质为良好的人数的概率.
名学生中体质为优秀的人数不少于体质为良好的人数的概率.
已知函数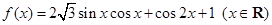 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 在
在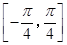 上的最小值,并写出
上的最小值,并写出 取最小值时相应的
取最小值时相应的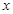 值.
值.