一个多面体的直观图和三视图如下: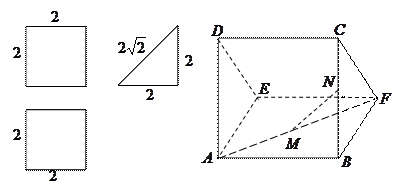
(其中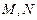 分别是
分别是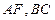 中点)
中点)
(1)求证: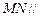 平面
平面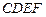 ;
;
(2)求多面体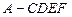 的体积.
的体积.
如图所示,平面 ∥平面
∥平面 ,点A∈
,点A∈ ,C∈
,C∈ ,点B∈
,点B∈ ,D∈
,D∈ ,点E,F分别在
,点E,F分别在 线段AB,CD上,且AE∶EB=CF∶FD.
线段AB,CD上,且AE∶EB=CF∶FD.
(1)求证:EF∥ ;
;
(2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,
求EF的长.
已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心.
(1)求证:平面G1G2G3∥平面ABC;
(2)求S△ ∶S△ABC.
∶S△ABC.
如图所示,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F, 且B1E=C1F.求证:EF∥平面ABCD.
且B1E=C1F.求证:EF∥平面ABCD.
如图所示,在三棱柱ABC—A1B1C1中,M、N分别是BC和A1B1的中点.
求证:MN∥平面AA1C1.
如图所示,在四面体ABCD中,E、F分别是线段AD、BC上的点, =
= =
= ,AB=CD=3,EF=
,AB=CD=3,EF= ,求AB、CD所成角的大小.
,求AB、CD所成角的大小.