(本小题满分12分)已知数列 是首项为
是首项为 且公比
且公比 不等于
不等于 的等比数列,
的等比数列, 是其前
是其前 项的和,
项的和, 成等差数列.
成等差数列.
(1)证明: 成等比数列;
成等比数列;
(2)求和:
命题 方程
方程 有两个不等的正实数根, 命题
有两个不等的正实数根, 命题 方程
方程 无实数根。若“
无实数根。若“ 或
或 ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。
函数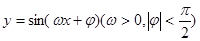 在同一个周期内,当
在同一个周期内,当 时,
时,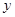 取最大值1,当
取最大值1,当 时,
时,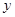 取最小值
取最小值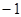 。
。
(1)求函数的解析式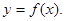
(2)函数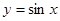 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到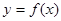 的图象?
的图象?
(3)若函数 满足方程
满足方程 求在
求在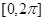 内的所有实数根之和.
内的所有实数根之和.
某港口海水的深度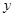 (米)是时间
(米)是时间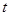 (时)(
(时)(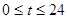 )的函数,记为:
)的函数,记为:
已知某日海水深度的数据如下:
 (时) (时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
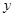 (米) (米) |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察, 的曲线可近似地看成函数
的曲线可近似地看成函数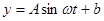 的图象
的图象
(I)试根据以上数据,求出函数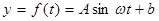 的振幅、最小正周期和表达式;
的振幅、最小正周期和表达式;
(II)一般情况下,船舶航行时,船底离海底的距离为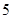 米或
米或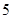 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为
米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为 米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
设向量 .
.
(Ⅰ)求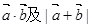 ;
;
(Ⅱ)若函数 ,求
,求 的最小值、最大值.
的最小值、最大值.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、
PC的中点.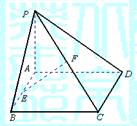
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°求EF与平面ABCD所成的角的大小.