如图,在四棱锥 中,底面
中,底面 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面 ,
, ,
,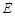 是
是 的中点,作
的中点,作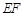 ⊥
⊥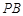 交
交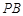 于点
于点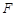 .
.
(1)证明: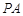 ∥平面
∥平面 ;
;
(2)证明: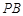 ⊥平面
⊥平面 .
.
过点 作倾斜角为
作倾斜角为 的直线与曲线
的直线与曲线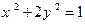 交于点
交于点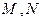 ,求
,求 最小值及相应的
最小值及相应的 值.
值.
为了让学生等多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表。请你根据频率分布表解答下列问题:
(1)填充频率分布表中的空格。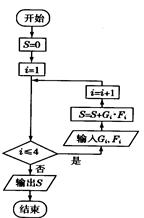
(2)为鼓励学生更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?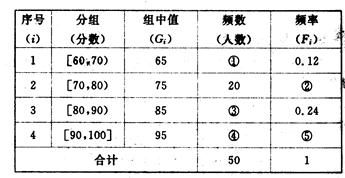
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.
设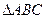 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且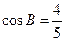 ,
,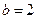 。
。
(1)当 时,求
时,求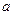 的值.
的值.
(2)当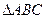 的面积为3时,求
的面积为3时,求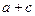 的值.
的值.
如图所示,已知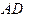 是
是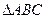 的外角
的外角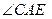 的平分线,交BC的延长线于点D,延长DA交
的平分线,交BC的延长线于点D,延长DA交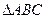 的外接圆于点F,连接FB,FC
的外接圆于点F,连接FB,FC
(1)求证: .
.
(2)求证: .
.
(3)若AB是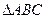 外接圆的直径,
外接圆的直径,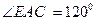 ,BC=6cm,求AD的长.
,BC=6cm,求AD的长.
对于函数 ,若存在
,若存在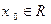 ,使得
,使得 成立,称
成立,称 为不动点,已知函数
为不动点,已知函数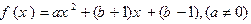
(1)当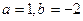 时,求函数
时,求函数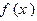 不动点.
不动点.
(2)若对任意的实数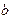 ,函数
,函数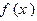 恒有两个相异的不动点,求a的取值范围.
恒有两个相异的不动点,求a的取值范围.