若数列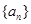 满足
满足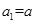 且
且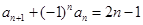 (其中
(其中 为常数),
为常数),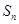 是数列
是数列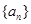 的前
的前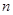 项和,数列
项和,数列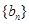 满足
满足 .
.
(1)求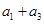 的值;
的值;
(2)试判断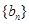 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;
(3)求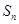 (用
(用 表示).
表示).
(本题满分12分)已知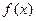 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设 ,
, ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求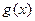 和
和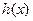 的定义域;(2)如果
的定义域;(2)如果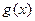 和
和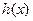 两个函数的定义域的交集为非空集合,求c的取值范围;(3)当
两个函数的定义域的交集为非空集合,求c的取值范围;(3)当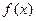 在其定义域内是奇函数,又是增函数时,求使
在其定义域内是奇函数,又是增函数时,求使 的自变量
的自变量 的取值范围.
的取值范围.
设函数 为奇函数,导函数
为奇函数,导函数 的最小值为-12,函数
的最小值为-12,函数 的图象在点P
的图象在点P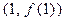 处的切线与直线
处的切线与直线 垂直.(1)求a,b,c的值;(2)求
垂直.(1)求a,b,c的值;(2)求 的各个单调区间,并求
的各个单调区间,并求 在
在 [-1, 3]时的最大值和最小值.
[-1, 3]时的最大值和最小值.
在等比数列 中,
中,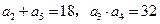 ,并且
,并且 (1)求
(1)求 以及数列
以及数列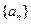 的通项公式;(2)设
的通项公式;(2)设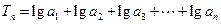 ,求当
,求当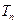 最大时
最大时 的值.
的值.
设函数 ,其中向量
,其中向量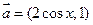 ,
, (1)求函数
(1)求函数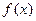 的最小正周期和单调递增区间;(2)当
的最小正周期和单调递增区间;(2)当 时,求函数
时,求函数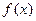 的值域.
的值域.
甲、乙两颗卫星同时监测台风,根据长期经验得知,甲、乙预报台风准确的概率分别为0.8和0.75.求:(1) 在同一次预报中,甲、乙两卫星只有一颗预报准确的概率;(2) 若甲独立预报4次,至少有3次预报准确的概率.