(本小题满分13分)对于给定数列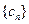 ,如果存在实常数
,如果存在实常数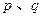 ,使得
,使得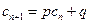 对于任意
对于任意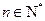 都成立,我们称数列
都成立,我们称数列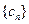 是 “M类数列”.
是 “M类数列”.
(I)若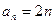 ,
,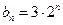 ,
,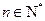 ,数列
,数列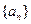 、
、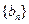 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数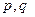 ,若不是,请说明理由;
,若不是,请说明理由;
(II)若数列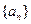 满足
满足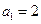 ,
,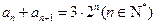 .
.
(1)求数列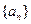 前
前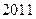 项的和.
项的和.
(2)已知数列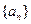 是 “M类数列”,求
是 “M类数列”,求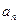 .
.
(本小题12分)在三角形ABC中, AB=2,BC=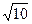 ,CA=3。点M是三角形ABC三边的高所在直线的交点。(I)求
,CA=3。点M是三角形ABC三边的高所在直线的交点。(I)求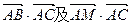 的值;(II)求满足关系式
的值;(II)求满足关系式 的实数p及q 值。
的实数p及q 值。
(本小题12分)已知递增的等比数列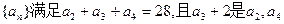 的等差中项。(1)求数列
的等差中项。(1)求数列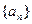 的通项公式;(2)若
的通项公式;(2)若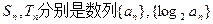 的前n项和,求
的前n项和,求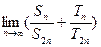 的值。
的值。
(本小题12分)某中学在高一开设了4门选修课,每个学生必须且只需选修1门选修课,对于该年级的甲、乙、丙3名学生,回答下列问题。(I)求这3名学生选择的选修课互不相同的概率;(II)求恰有2门选修课没有被这3名学生选择的概率;(III)某一选修课被这3名学生选择的人数的数学期望。
(本小题10分)已知向量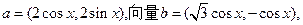
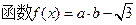 (1)求函数
(1)求函数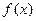 的最小正周期;(2)求函数
的最小正周期;(2)求函数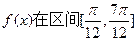 上的值域。
上的值域。
【理科】已知函数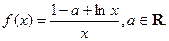
(I)求 的极值;
的极值;
(II)若 的取值范围;
的取值范围;
(III)已知