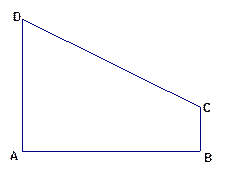
如图,四边形 是直角梯形,∠
是直角梯形,∠ =90°,
=90°,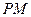 ∥
∥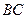 ,
,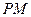 =1,
=1,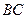 =2,又
=2,又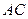 =1,∠
=1,∠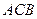 =120°,
=120°,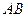 ⊥
⊥ ,直线
,直线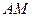 与直线
与直线 所成的角为60°.
所成的角为60°.
(1)求证:平面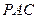 ⊥平面
⊥平面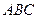 ;
;
(2)求三棱锥 的体积;
的体积;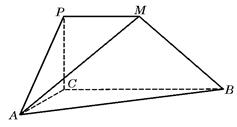
如图,四棱锥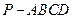 中,底面
中,底面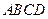 是平行四边形,
是平行四边形,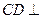 侧面
侧面 ,点在侧棱
,点在侧棱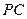 上,
上,
且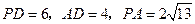 .
.
(1)求证:平面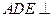 平面
平面 ;
;
(2)若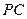 与
与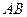 所成角为
所成角为 ,二面角
,二面角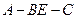 的大小为
的大小为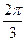 ,求
,求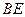 与平面
与平面 所成角的大小.
所成角的大小.
设 的内角
的内角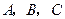 所对的边长分别为
所对的边长分别为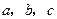 ,已知
,已知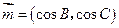 ,
,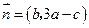 ,且
,且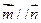 .
.
(1)求 的值;
的值;
(2)若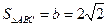 ,求
,求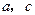 的值.
的值.
已知函数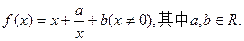
(1)若曲线 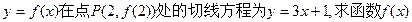 的解析式:
的解析式:
(2)讨论函数 的单调性;
的单调性;
(3)若对于任意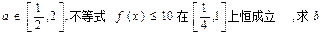 的取值范围
的取值范围
已知点(1,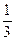 )是函数
)是函数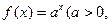 且
且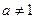 )的图象上一点,等比数列
)的图象上一点,等比数列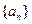 的前项和为
的前项和为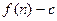 ,数列
,数列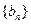
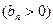 的首项为,且前项和
的首项为,且前项和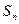 满足
满足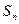 -
-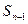 =
=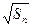 +
+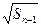 (
(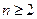 ).
).
(1)求数列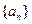 和
和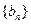 的通项公式;
的通项公式;
(2)若数列{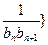 前项和为
前项和为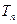 ,问
,问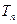 >
>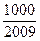 的最小正整数是多少?
的最小正整数是多少?
如图,在直角梯形 中,
中,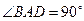 ,
,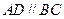 ,
,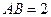 ,
,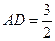 ,
,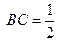 ,椭圆以
,椭圆以 、
、 为焦点且经过点
为焦点且经过点 .
.
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)以该椭圆的长轴为直径作圆,判断点C与该圆的位置关系。