(本小题满分12分)
某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……,依等差数列逐年递增.
(Ⅰ)设使用n年该车的总费用(包括购车费用)为f(n),试写出f(n)的表达式;
(Ⅱ)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少)。
(本小题满分15分)已知函数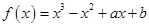 (
(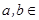 R)的一个极值点为
R)的一个极值点为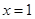 .
.
(1) 求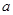 的值和
的值和 的单调区间;
的单调区间;
(2)若方程 的两个实根为
的两个实根为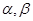
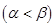 , 函数
, 函数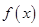 在区间
在区间 上单调,求
上单调,求 的取值范围。
的取值范围。
(本小题满分14分)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到DA1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小。
(本小题满分14分)设数列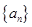 的前
的前 项和为
项和为 ,已知
,已知 ,
,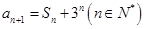
(1)令 求证:
求证: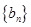 是等比数列;
是等比数列;
(2)令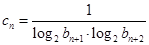 ,设
,设 是数列
是数列 的的前
的的前 项和,求满足不等式
项和,求满足不等式 的
的 的最小值。
的最小值。
(本小题满分14分)
已知函数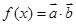 ,其中
,其中
(1)求函数 在区间
在区间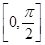 上的单调递增区间和值域;
上的单调递增区间和值域;
(2)在 中,
中, ,
,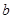 ,
, 分别是角
分别是角 的对边,
的对边, ,且
,且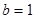
 的面积
的面积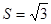 ,求边
,求边 的值.
的值.
已知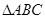 的三个顶点在抛物线
的三个顶点在抛物线 上,
上,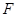 是抛物线的焦点,且
是抛物线的焦点,且 ,
, .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)若直线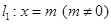 与上述抛物线相交于
与上述抛物线相交于 点,直线
点,直线 过点
过点 且与
且与 处的切线垂直. 求证:直线
处的切线垂直. 求证:直线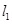 关于直线
关于直线 的对称直线经过定点.
的对称直线经过定点.