（本小题满分14分）在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE:EB＝CF:FA＝CP:PB＝1:2（如图1）。将△AEF沿EF折起到DA1EF的位置，使二面角A1－EF－B成直二面角，连结A1B、A1P（如图2）
（Ⅰ）求证：A1E⊥平面BEP；
（Ⅱ）求直线A1E与平面A1BP所成角的大小。
如图，PA⊥平面ABCD，矩形ABCD的边长AB=1，BC=2，E为BC的中点．
（1）证明：PE⊥DE；
（2）如果PA=2，求异面直线AE与PD所成的角的大小．
已知直线l：3x+4y-2=0
（Ⅰ）求经过直线l与直线x+3y-4=0的交点P，且垂直于直线x-2y-1=0的方程；
（Ⅱ）求直线l与两坐标轴围成的三角形的内切圆的方程．
（本小题满分14分）已知函数
，其中
．
（1）求
的单调区间；
（2）求证：
＜
（本小题满分13分）设椭圆C1：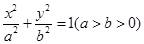
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：
与y轴的交点为B，且经过F1，F2点．
（1）求椭圆C1的方程；
（2）设M（0，
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值．
（本小题满分12分）如图，在四棱锥P—ABCD中，平面PAB⊥平面ABCD，AD∥BC，∠ABC＝90°，PA＝PB＝3，BC＝1，AB＝2，AD＝3，O是AB中点。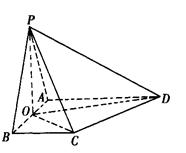
（1）证明CD⊥平面POC；
（2）求二面角C—PD—O的平面角的余弦值。