已知函数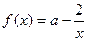 。
。
(Ⅰ)讨论 的奇偶性;
的奇偶性;
(Ⅱ)判断 在
在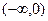 上的单调性并用定义证明。
上的单调性并用定义证明。
在数列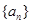 中,
中,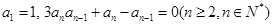 .
.
(1)求数列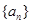 的通项;
的通项;
(2)若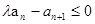 对任意的正整数
对任意的正整数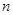 恒成立,求实数
恒成立,求实数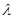 的取值范围.
的取值范围.
(本题满分l4分)已知向量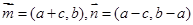 ,且
,且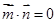 ,其中
,其中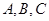 是
是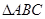 的三内角,
的三内角,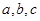 分别是角
分别是角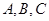 的对边.
的对边.
(1)求角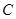 的大小;(2)求
的大小;(2)求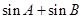 的取值范围.
的取值范围.
设A(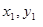 ),B(
),B(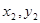 )是椭圆
)是椭圆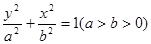 的两点,
的两点,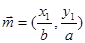 ,
,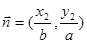 ,且
,且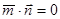 ,椭圆的离心率
,椭圆的离心率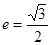 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1)求椭圆方程;
(2)若存在斜率为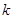 的直线AB过椭圆的焦点F(
的直线AB过椭圆的焦点F(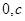 )(
)(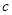 为半焦距),求
为半焦距),求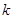 的值;
的值;
(3)试问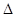 AOB的面积是否为定值?若是,求出该定值;若不是,说明理由。
AOB的面积是否为定值?若是,求出该定值;若不是,说明理由。
已知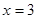 是函数
是函数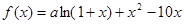 的一个极值点。
的一个极值点。
(1)求 ;(2)求函数
;(2)求函数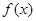 的单调区间;
的单调区间;
(3)若直线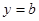 与函数
与函数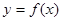 的图象有3个交点,求
的图象有3个交点,求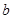 的取值范围。
的取值范围。
(12)设焦点在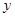 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为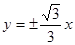 ,且离心率为2,已知点A(
,且离心率为2,已知点A(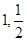 )
)
(1)求双曲线的标准方程;
(2)过点A的直线L交双曲线于M,N两点,点A为线段MN的中点,求直线L方程。