(本小题满分14分)
已知二次函数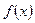 满足:
满足: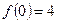 ,
,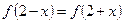 ,且该函数的最小值为1.
,且该函数的最小值为1.
⑴ 求此二次函数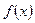 的解析式;
的解析式;
⑵ 若函数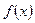 的定义域为
的定义域为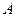 =
= 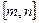 .(其中
.(其中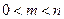 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数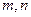 ,使得函数
,使得函数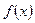 的值域也为
的值域也为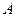 ?若存在,求出
?若存在,求出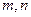 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本题满分10分)设函数 ,求:
,求:
(1) ;(2)
;(2) ;(3)函数
;(3)函数 .
.
(本题满分12分)若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 接近
接近 .
.
(1)若 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 接近
接近 ;
;
(3)已知函数 的定义域
的定义域 .任取
.任取 ,
, 等于
等于 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
(本题满分10分)甲乙两地相距 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为 ,固定部分为
,固定部分为 元.
元.
(1)把全程运输成本 (元)表示为
(元)表示为 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(本题满分10分)用定义证明函数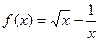 在定义域上是增函数.
在定义域上是增函数.
(本题满分10分) 求函数 在区间
在区间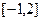 上的最大值和最小值,并指出何时取得最值.
上的最大值和最小值,并指出何时取得最值.