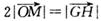在海岸A处,发现北偏东 方向,距离A为
方向,距离A为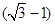 海里的B处有一走私船,在A北偏西
海里的B处有一走私船,在A北偏西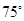 方向距离A为2海里的C处有我方一艘缉私艇奉命以
方向距离A为2海里的C处有我方一艘缉私艇奉命以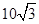 海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以
海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以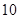 海里/小时的速度从B处向北偏东
海里/小时的速度从B处向北偏东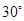 方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
已知等差数列{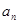 },
},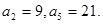
(Ⅰ)求{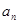 }的通项公式;
}的通项公式;
(Ⅱ)令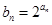 ,求数列
,求数列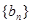 的前n项和Sn
的前n项和Sn
已知函数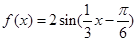 ,
,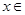
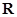 .
.
(1)求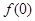 的值;
的值;
(2)设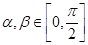 ,
,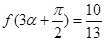 ,
,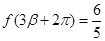 ,求
,求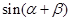 的值.
的值.
已知函数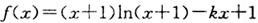 ,,k为常数,e是自然对数的底数).
,,k为常数,e是自然对数的底数).
(I)当k=1时,求f(x)的最小值;
(II)探求是否存在整数k使得f(X)在区间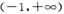 上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
(III)设函数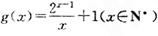 ,记
,记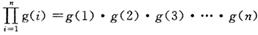 ,求证:
,求证: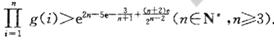
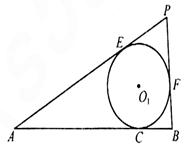
如图,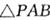 的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且
的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且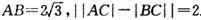 •
•
(I) 建立适当的平面直角坐标系,求动点p的轨迹w的方程;
(II) 设l是既不与AB平行也不与AB垂直的直线,线段AB的中点O到直线l的距离为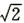 ,若l与曲线W相交于不同的两点G、H,点M满足
,若l与曲线W相交于不同的两点G、H,点M满足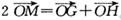 ,证明:
,证明: