已知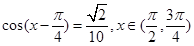 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求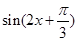 的值.
的值.
已知函数 ,
,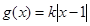 .
.
(Ⅰ)已知 ,若
,若 ,求
,求 的值;
的值;
(Ⅱ)设 ,当
,当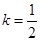 时,求
时,求 在
在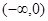 上的最小值;
上的最小值;
(Ⅲ)求函数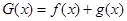 在区间
在区间 上的最大值.
上的最大值.
设函数 ,
,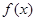 是定义域为
是定义域为 的奇函数.
的奇函数.
(Ⅰ)求 的值,判断并证明当
的值,判断并证明当 时,函数
时,函数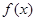 在
在 上的单调性;
上的单调性;
(Ⅱ)已知 ,函数
,函数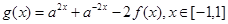 ,求
,求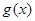 的值域;
的值域;
(Ⅲ)已知 ,若
,若 对于
对于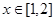 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数 .
.
已知函数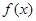 是定义域为R的奇函数.当
是定义域为R的奇函数.当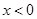 时,
时, ,图像如图所示.
,图像如图所示.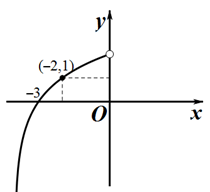
(Ⅰ)求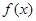 的解析式;
的解析式;
(Ⅱ)若方程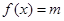 有两解,写出
有两解,写出 的范围;
的范围;
(Ⅲ)解不等式 ,写出解集.
,写出解集.
在不考虑空气阻力的情况下,火箭的最大速度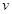 (单位:
(单位: )和燃料的质量
)和燃料的质量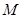 (单位:
(单位: ),火箭(除燃料外)的质量
),火箭(除燃料外)的质量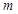 (单位:
(单位: )满足
)满足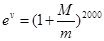 .(
.( 为自然对数的底)
为自然对数的底)
(Ⅰ)当燃料质量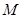 为火箭(除燃料外)质量
为火箭(除燃料外)质量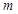 两倍时,求火箭的最大速度(单位:
两倍时,求火箭的最大速度(单位: );
);
(Ⅱ)当燃料质量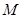 为火箭(除燃料外)质量
为火箭(除燃料外)质量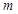 多少倍时,火箭的最大速度可以达到8
多少倍时,火箭的最大速度可以达到8 .(结果精确到个位,数据:
.(结果精确到个位,数据: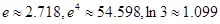 )
)
已知二次函数 的图像顶点为
的图像顶点为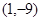 ,且图像在
,且图像在 轴截得的线段长为6.
轴截得的线段长为6.
(Ⅰ)求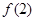 ;
;
(Ⅱ)若 在区间
在区间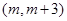 上单调,求
上单调,求 的范围.
的范围.