已知函数 在
在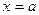 处取得极值.
处取得极值.
(Ⅰ) 求 ;
;
(Ⅱ) 设函数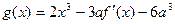 ,如果
,如果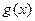 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数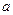 的取值范围.
的取值范围.
已知函数  ,
, .
.
(Ⅰ)当 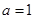 时,求函数
时,求函数  的最小值;
的最小值;
(Ⅱ)当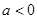 时,讨论函数
时,讨论函数  的单调性;
的单调性;
(Ⅲ)是否存在实数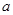 ,对任意的
,对任意的  ,且
,且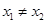 ,有
,有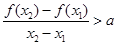
恒成立,若存在求出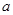 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
国际上钻石的重量计量单位为克拉.已知某种钻石的价值y (美元)与其重量x (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)若把一颗钻石切割成重量比为1∶3的两颗钻石,求价值损失的百分率;
(Ⅲ)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为m 克拉和n克拉,
试证明:当m="n" 时,价值损失的百分率最大.
(注:价值损失的百分率= ×100% ;在切割过程中的重量损耗忽略不计)
×100% ;在切割过程中的重量损耗忽略不计)
已知函数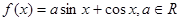 ;
;
(Ⅰ)若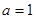 ,求过点
,求过点 的切线方程;
的切线方程;
(Ⅱ)若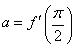 ,求
,求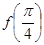 的值.
的值.
已知函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时,
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
已知集合 ,
,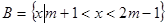
(Ⅰ)若 =5,求
=5,求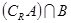 ;
;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.