(本小题满分12分)如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=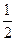 PD.
PD.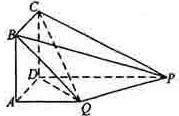
(I) 证明:PQ⊥平面DCQ;
(II)求棱锥Q—ABCD的的体积与棱锥P—DCQ的体积的比值.
统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在
(1)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中用分层抽样方法抽出100人作进一步分析,则月收入在 的应抽取多少人;
的应抽取多少人;
(2)根据频率分布直方图估计样本数据的中位数.
如图,在平行四边形 中,边
中,边 所在直线的方程为
所在直线的方程为 ,点
,点 .
.
(1)求直线 的方程;
的方程;
(2)求 边上的高
边上的高 所在直线的方程.
所在直线的方程. 
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,用茎叶图分别记录抽查数据如下:
(1)分别求出甲、乙两组数据的中位数;
(2)估计哪个车间的产品平均重量较高,哪个车间比较稳定.
已知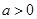 ,函数
,函数 (其中
(其中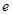 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求函数 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)设数列 的通项
的通项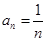 ,
,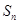 是前
是前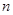 项和,证明:
项和,证明: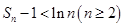 .
.
设动点
 到定点
到定点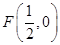 的距离比到
的距离比到 轴的距离大
轴的距离大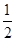 .记点
.记点 的轨迹为曲线C.
的轨迹为曲线C.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ)设圆M过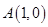 ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上,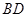 是圆M在
是圆M在 轴的截得的弦,当M运动时弦长
轴的截得的弦,当M运动时弦长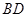 是否为定值?说明理由;
是否为定值?说明理由;
(Ⅲ)过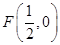 作互相垂直的两直线交曲线C于G、H、R、S,求四边形面
作互相垂直的两直线交曲线C于G、H、R、S,求四边形面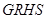 的最小值.
的最小值.