如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF交CD于G,求∠1的度数。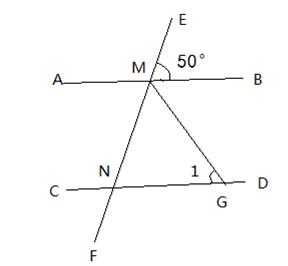
已知:∠ (不写作法,保留作图痕迹)求作:∠
(不写作法,保留作图痕迹)求作:∠ ,使得∠
,使得∠ ∠
∠ .
.
如图 ,在Rt 中,
中, ,M为AB边上中点,将Rt
,M为AB边上中点,将Rt 绕点M旋转,使点C与点A重合得Rt
绕点M旋转,使点C与点A重合得Rt ,设AE交CB于点N.
,设AE交CB于点N.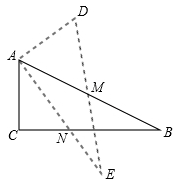
(1)若 ,求
,求 的度数;
的度数;
(2)若AC=2,BC=5,求CN的长.
如图抛物线 与
与 轴交于A(1,0),
轴交于A(1,0), 两点
两点 
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交 轴于
轴于 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点 ,使得
,使得 的周长最小?若存在,求出
的周长最小?若存在,求出 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
大润发超市进了一批成本为8元/个的文具盒。调查发现: 这种文具盒每个星期的销售量 个)与它的定价
个)与它的定价 (元/个)的关系如图所示:
(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量 个)与它的定价
个)与它的定价 (元/个)之间的函数关系式(不必写出自变量
(元/个)之间的函数关系式(不必写出自变量 的取值范围)
的取值范围)
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每个月就可以多售出5件。
(1 )降价前商场每个月销售该商品的利润是多少?
(2)要使商场每月销售这种商品的利润达到7200元,更有利于减少库存,则每件商品降价多少元?