某中学开展“五比五创”演讲比赛活动,九(1)班准备根据根据平时练习成绩准备从张华、李明2名选手选出一名参加比赛,他们两人的五次平时成绩(满分20分)如下图所示。
(1)根据下图,分别求出张华、李明的平均成绩和方差;
(2)根据(1)的计算结果,分析张华、李明同学各自的优点,并决定让那位同学参加比赛?
先化简代数式 ÷(x+2﹣
÷(x+2﹣ );再从方程y2﹣3y+2=0的根中选择一个合适的作为x的值,求出原代数式的值.
);再从方程y2﹣3y+2=0的根中选择一个合适的作为x的值,求出原代数式的值.
如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB﹣﹣BC﹣﹣CD所示(不包括端点A).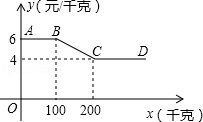
(1)当100<x<200时,求y与x之间的函数关系式.
(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?
(3)在(2)的条件下,求经销商一次性采购的蔬菜是多少千克时,蔬菜种植基地能获得418元的利润?
如图,在矩形ABCD中,AB=4,AD=10.一把三角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
(1)证明△DPC∽△AEP;
(2)当∠CPD=30°时,求AE的长;
(3)是否存在这样的点P,使△DPC的周长等于△AEP周长的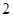 倍?若存在,求出DP的长;若不存在,请说明理由.
倍?若存在,求出DP的长;若不存在,请说明理由.
已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AD为弦作⊙O,使圆心O在AB上.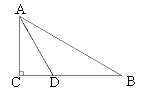
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;
(2)求证:BC为⊙O的切线.