问题再现
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.
我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如右图中，用正方形镶嵌平面，可以发现在一个顶点O周围围绕着4个正方形的内角.
试想：如果用正六边形来镶嵌平面，在一个顶点周围应该围绕着 个
正六边形的内角．
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：
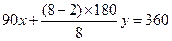，整理得：
，
我们可以找到惟一一组适合方程的正整数解为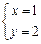
．
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．
验证2：
结论2：
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．
问题拓广
请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．
猜想3： .
验证3：
结论3：
.
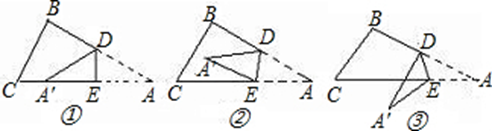
如图①，一张三角形ABC纸片，点D、E分别是△ABC边上两点．
研究（1）：如果沿直线DE折叠，使A点落在CE上，则∠BDA′与∠A的数量关系是__ ▲_________
∠BDA′=2∠A
∠BDA′+∠CEA′=2∠A如果折成图②的形状，猜想∠BDA′、∠CEA和∠A的数量关系是__ ▲_________
如果折成图③的形状，猜想∠BDA′、∠CEA′和∠A的数量关系，并说明理由．
猜想：▲________将问题1推广，如图，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间的数量关系是_ ▲________
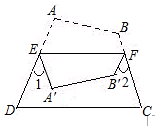
如图，BD是∠ABC的平分线，DE//CB，交AB于点E，∠A＝45°，
∠BDC＝60°，求△BDE各内角的度数．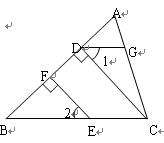
在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．（１）请画出平移后的△A′B′C′．（２）求△A′B′C′的面积．
已知代数式x2＋px＋q，当x＝1时，代数式的值为2；当x＝－2时，代数式的值为11．求p、q的值
求当x＝
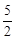时，该代数式的值．
解方程组