（本题6分）某人去水果批发市场采购苹果，他看中了Ａ、Ｂ两家苹果。这两家苹果品质一样，零售价都为６元／千克，批发价各不相同。
Ａ家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠。
B家的规定如下表：
| 数量范围（千克） |
0～500 |
500以上～1500 |
1500以上～2500 |
2500以上 |
| 价 格（元） |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【表格说明：批发价格分段计算，如：某人批发苹果2100千克，则总费用=6×95%×500+6×85%×1000+6×75%×（2100－1500）】
（1）如果他批发600千克苹果，则他在A 家批发需要 元，在B家批发需要 元；
(2) 如果他批发x千克苹果(1500＜x＜2000)，则他在A 家批发需要 元,在B家批发需要 元(用含x的代数式表示)；
(3) 现在他要批发1800千克苹果，你能帮助他选择在哪家批发更优惠吗?请说明理由。
如图， AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．
（1）求证：AD=AE；
(2) 连接OA，BC，试判断直线OA，BC的关系，并说明理由．
解不等式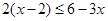
，并写出它的正整数解.
如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（2，3）．双曲线y=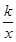
（x＞0）的图象经过BC的中点D，且与AB交于点E，连接DE．
（1）求k的值及点E的坐标；
（2）若点F是OC边上一点，且△FBC∽△DEB，求直线FB的解析式．
如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．
（1）求证：△ADC≌△ECD；
（2）若BD=CD，求证：四边形ADCE是矩形．
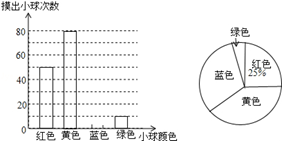
一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球，小球除颜色外完全相同，为估计该口袋中四种颜色的小球数量，每次从口袋中随机摸出一球记下颜色并放回，重复多次试验，汇总实验结果绘制如图不完整的条形统计图和扇形统计图．
根据以上信息解答下列问题：
（1）求实验总次数，并补全条形统计图；
（2）扇形统计图中，摸到黄色小球次数所在扇形的圆心角度数为多少度？
（3）已知该口袋中有10个红球，请你根据实验结果估计口袋中绿球的数量．