(本小题满分13分)已知函数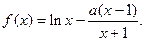 (
(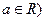
(1)若函数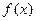 在定义域上为单调增函数,求
在定义域上为单调增函数,求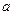 的取值范围;
的取值范围;
(2)设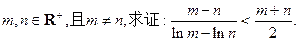
本题满分10分)
设函数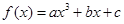
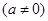 为奇函数,其图象在点
为奇函数,其图象在点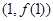 处的切线与直线
处的切线与直线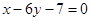 垂直,导函数
垂直,导函数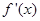 的最小值为
的最小值为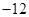 .试求
.试求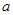 ,
, ,
, 的值。
的值。
已知函数
 .
.
(1)求 的定义域;
的定义域;
(2)讨论 的奇偶性;
的奇偶性;
(3)讨论 在
在 上的单调性.
上的单调性.
若非零函数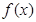 对任意实数
对任意实数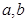 均有
均有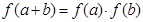 ,且当
,且当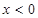 时,
时, 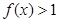 ;
;
(1)求证: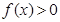 (2)求证:
(2)求证: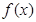 为减函数
为减函数
(3)当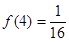 时,解不等式
时,解不等式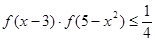
武汉市某地西瓜从2012年6月1日起开始上市。通过市场调查,得到西瓜种植成本Q(单位:元/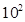 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表:
| 时间t |
50 |
110 |
250 |
| 种植成本Q |
150 |
108 |
150 |
求:1)根据上表数据,从下列函数中选取一个函数描述西瓜种植成本Q与上市时间t的变化关系。
Q=at+b, Q=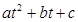 , Q= a
, Q= a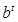 , Q=a
, Q=a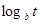 .
.
2)利用你选取的函数,求西瓜种植成本最低时的上市天数及最低种植成本。
已知-1≤x≤2,求函数f(x)=3+2·3x+1-9x的值域.