如图，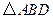 
和
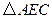均为等边三角形，连接BE、CD．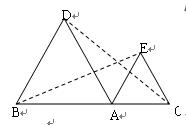
（1）请判断：线段BE与CD的大小关系是 ；
（2）观察图，当
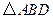和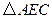分别绕点A旋转时，BE、CD之间的大小关系是否会改变?
（3）观察图3和4，若四边形ABCD、DEFG都是正方形,猜想类似的结论是 ,在图4中证明你的猜想.
（4）这些结论可否推广到任意正多边形（不必证明）,如图5,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点，连接图中哪两个顶点,能构造出两个全等三角形？
和△
中，∠
=∠
是
的中点，
⊥
于
，且
．
=
；
，求
的长．
, 求这个多边形的边数及内角和.
