如图, 等腰梯形ABCD中,AB=15,AD=20,∠C=30º.点M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动.
(1)设ND的长为x,用x表示出点N到AB的距离,并写出x的取值范围.
(2)当五边形BCDNM面积最小时,请判断△AMN的形状.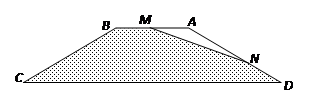
某化工材料经销公司购进了一种化工原料共7000kg,购进价格为每千克30元,物价部门规定其销售单价不得高于每千克70元,也不得低于30元,市场调查发现:单价定为70元时,日均销售60kg;单价每降低1元,日均多售出2kg,在销售过程中,每天还要除去其他费用400元(天数不足一天时,按整天计算).设销售单价为x元,日均获利为y元. (日均获利=销售所得利润-各种开支)
(1)求y关于x的函数关系式并写出x的取值范围.
(2)求每千克单价定为多少元时日均获利最多,是多少?
(3)若用日均获利最多的方式销售或按销售单价最高销售,试比较哪一种销售获总利更多,多多少?
张大伯计划建一个面积为72平方米的矩形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分(包括中间的隔墙)用30米的竹篱笆围成,如图。
(1).请你通过计算帮助张大伯设计出围养鸡场的方案.
(2).在上述条件不变的情况下,能围出比72平方米更大的养鸡场吗?请说明理由。
先化简(6x +
+ 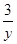
 -(4y
-(4y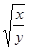 +
+ 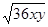 )再求值,其中
)再求值,其中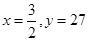
先阅读,后解答:
像上述解题过程中, 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1) 的有理化因式是;
的有理化因式是; 的有理化因式是。
的有理化因式是。
(2)将下列式子进行分母有理化:
① =;②
=;② =。
=。
(3)已知 ,比较
,比较 与
与 的大小关系。
的大小关系。