如图,圆锥的母线长为6cm,其侧面展开图是半圆,求: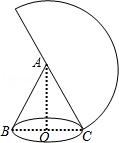
(1)圆锥的底面半径;
(2)∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
在平面直角坐标系中,△ABC三个顶点的坐标分别是A(3,6)、B(1,4)、C(1,0).
(1)△ABC外接圆的圆心坐标是;
(2)求以BC为轴,将△ABC旋转一周所得几何体的全面积(即求所有表面的面积之和,结果保留根号和π)
小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径OB=3cm,高OC=4cm,求这个圆锥形漏斗的侧面积.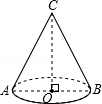
已知圆锥的底面直径是8,母线长是16,求它的侧面展开图的圆心角与圆锥的全面积.
如图,已知每个小正方形的边长为1cm,O、A、B都在小正方形顶点上,扇形OAB是某个圆锥的侧面展开图.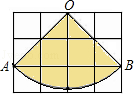
(1)计算这个圆锥侧面展开图的面积;
(2)求这个圆锥的底面半径.