(本小题满分12分), (Ⅰ)小问5分,(Ⅱ)小问7分.)
已知函数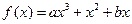 (其中常数a,b∈R),
(其中常数a,b∈R), 是奇函数.
是奇函数.
(Ⅰ)求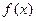 的表达式;
的表达式;
(Ⅱ)讨论 的单调性,并求
的单调性,并求 在区间上的最大值和最小值.
在区间上的最大值和最小值.
(本小题满分12分)
计算机考试分理论考试与上机操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中合格的概率分别为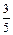 ,
,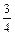 ,
,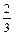 ;在上机操作考试中合格的概率分别为
;在上机操作考试中合格的概率分别为 ,
,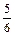 ,
,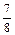 .所有考试是否合格相互之间没有影响.
.所有考试是否合格相互之间没有影响.
(Ⅰ)甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大?
(Ⅱ)求这三人计算机考试都获得“合格证书”的概率;
(Ⅲ)用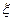 表示甲、乙、丙三人在理论考核中合格人数,求
表示甲、乙、丙三人在理论考核中合格人数,求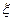 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分12分)
已知数列{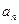 },其前n项和Sn满足Sn+1=2
},其前n项和Sn满足Sn+1=2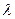 Sn+1(
Sn+1(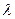 是大于0的常数),且a1=1,a3=4.
是大于0的常数),且a1=1,a3=4.
(Ⅰ)求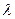 的值;
的值;
(Ⅱ)求数列{an}的通项公式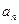 ;
;
24.选修4-5:不等式选讲
若关于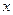 的方程
的方程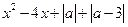 =0有实根
=0有实根
(1)求实数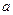 的取值集合
的取值集合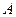
(2)若存在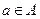 ,使得不等式
,使得不等式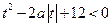 成立,求实数
成立,求实数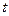 的取值范围。
的取值范围。
.选修4—4:坐标系与参数方程
以平面直角坐标系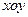 的原点
的原点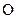 为极点,
为极点,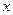 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线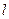 的极坐标方程为
的极坐标方程为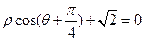 ,曲线
,曲线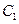 的参数方程为
的参数方程为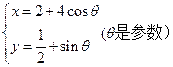
(1)若把曲线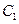 上的横坐标缩短为原来的
上的横坐标缩短为原来的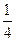 ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线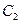 ,
,
求曲线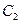 在直角坐标系下的方程
在直角坐标系下的方程
(2)在第(1)问的条件下,判断曲线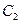 与直线
与直线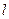 的位置关系,并说明理由;
的位置关系,并说明理由;
22.选修4-1:几何证明选讲
如图:四边形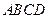 是边长为
是边长为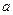 的正方形,以
的正方形,以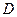 为圆心,
为圆心,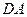 为半径的圆弧与以
为半径的圆弧与以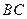 为直径的圆
为直径的圆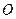 交于点
交于点 ,连接
,连接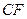 并延长
并延长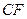 交于
交于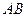 点
点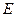
(1)求证: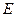 是
是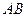 的中点
的中点
(2)求线段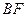 的长
的长