计算：
如图，从左到右，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所有整数之和都相等。
（I）可求得
，第
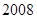个格子中的数为__________；（II）判断：前
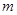个格子中所填整数之和是否可能为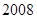？若能，求出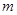的值；若不能，请说明理由；（III）如果
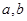为前三个格子中的任意两个数，那么所有的
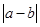的和可以通过计算|
★|+|☆|+|★
☆|+|★
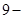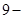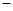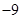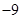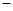|+|☆|+|☆★|得到，若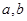为前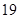
个格子中的任意两个数，则所有的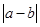的和为__________.
如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线。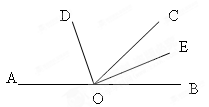
（1）求∠DOE的度数。
（2）如果∠AOD=60°。求∠BOE的度数？
如图，已知C是AB的中点，D是AC的中点，E是BC的中点．若DE=9cm，求AB的长；
在“旧城改造”中，小明家搬进了政府提供的安置房，这个小区都用管道天燃气，为了估算第一个月使用天然气的开支情况，从10月15日小强连续5天每天晚上记录了天然气表的读数。
| 日期 |
15 |
16 |
17 |
18 |
19 |
天然气表显示读数（ ） |
219 |
229 |
241 |
249 |
259 |
小明妈妈10月15日买了一张面值500元的天然气使用卡，若天然气价格是2.32元/m3,请你估算这张卡够小明家用一个月吗？（按30天计算）
某食品厂从生产的食品罐头中抽出20听检测质量. 将超过标准的质量用正数表示，不足标准的质量用负数表示，结果记录如下表：
| 与标准质量的偏差 （单位：克） |
-10 |
-5 |
0 |
+5 |
+10 |
+15 |
| 听数 |
1 |
3 |
6 |
6 |
3 |
1 |
问这批样品的平均质量比标准质量多还是少？相差多少克？
某条河河流目前的水位是4.5m，超过警戒线1.5m，预测未来3天平均每天下降0.55m. 试问预计3天后该河流的水位线是多少米？是否已低于警戒线？