如图,已知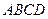 为平行四边形,
为平行四边形,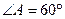 ,
,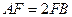 ,
,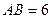 ,点
,点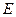 在
在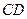 上,
上, ,
, ,
,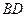 交
交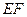 于点
于点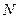 ,现将四边形
,现将四边形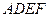 沿
沿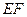 折起,使点
折起,使点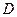 在平面
在平面 上的射影恰在直线
上的射影恰在直线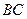 上.
上.
(Ⅰ) 求证: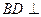 平面
平面 ;
;
(Ⅱ) 求折后直线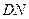 与直线
与直线 所成角的余弦值;
所成角的余弦值;
(Ⅲ) 求三棱锥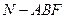 的体积.
的体积.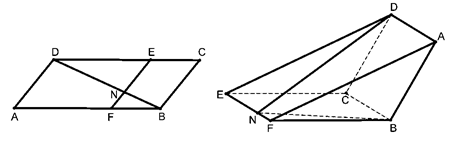
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时)飞机先看到山顶的俯角为150,经过420s(秒)后又看到山顶的俯角为450,求山顶的海拔高度(取 =1.4,
=1.4,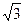 =1.7).
=1.7).
|

已知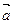 =(1,2),
=(1,2),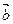 =(-3,2),当k为何值时,
=(-3,2),当k为何值时,
(1)k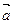 +
+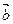 与
与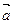 -3
-3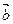 垂直;
垂直;
(2)k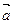 +
+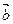 与
与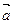 -3
-3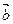 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
已知函数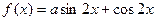 ,且
,且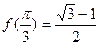 .
.
(1)求a的值和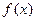 的最大值;
的最大值;
(2)问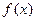 在什么区间上是减函数.
在什么区间上是减函数.
设两个非零向量 、
、 不共线,如果
不共线,如果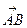 =
= +
+ ,
,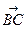 =2
=2 +8
+8 ,
,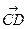 =3(
=3( -
- ),求证A、B、D三点共线.
),求证A、B、D三点共线.
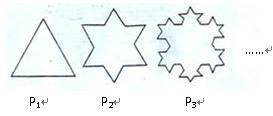
(本小题10分)“雪花曲线”因其形状类似雪花而得名,它可以以下列方式产生,如图,有一列曲线 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形,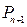 是对
是对 进行如下操作得到:将
进行如下操作得到:将 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(
的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉( ).
).
(1)记曲线 的边长和边数分别为
的边长和边数分别为 和
和 (
(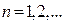 ),求
),求 和
和 的表达式;
的表达式;
(2)记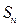 为曲线
为曲线 所围成图形的面积,写出
所围成图形的面积,写出 与
与 的递推关系式,并求
的递推关系式,并求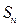 .
.