某城市按以下规定收取每月煤气费:用煤气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费. 如甲用户某月份用煤气80每立方米,那么这个月甲用户应交煤气费用为60×0.8+(80-60)×1.2=72元.设甲用户某月用煤气x立方米,用含x的代数式表示甲用户该月的煤气费.
若x≤60,则费用表示为 ;
若x>60,则费用表示为 .若甲用户10月份的煤气费是84元,求甲用户10月份用去煤气多少立方米?
如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧 上一点,连接BD,AD,OC,∠ADB=30°.
上一点,连接BD,AD,OC,∠ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6cm,求图中阴影部分的面积.
某汽车销售公司6月份销售某厂家汽车,在一定范围内,每辆汽车的进价与销售量有如下关系,若当月仅售出1辆汽车,则该汽车的进价为27万元;每多售出1辆,所有售出的汽车的进价均降低0.1万元/辆,月底厂家根据销售量一次性返利给销售公司,销售量在10辆以内(含10辆),每辆返利0.5万元,销售量在10辆以上,每辆返利1万
(1)若该公司当月售出3辆汽车,则每辆汽车的进价为万元;
(2)如果汽车的售价为28万元/辆,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
如图,已知直线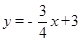 与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.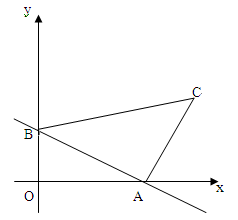
(1)求△AOB的面积;
(2)求点C坐标;
(3)点P是x轴上的一个动点,设P(x,0)
①请用x的代数式表示PB2、PC2;
②是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;
如果存在,请求出点P的坐标.
“十一黄金周”的某一天,小刚全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩,该小汽车离家的路程S(千米)与时间t (时)的关系可以用右图的折线表示。根据图象提供的有关信息,解答下列问题: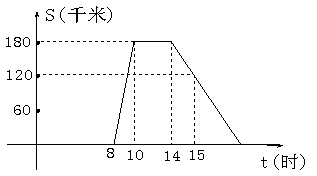
(1)小刚全家在旅游景点游玩了多少小时?
(2)求出整个旅程中S(千米)与时间t (时)的函数关系式,并求出相应自变量t的取值范围。
(3)小刚全家在什么时候离家120㎞?什么时候到家?
某软件公司开发出一种图书管理软件,前期投入的各种费用总共50000元,之后每售出一套软件,软件公司还需支付安装调试费用200元,设销售套数x(套)。
(1)试写出总费用y(元)与销售套数x(套)之间的函数关系式.
(2)该公司计划以400元每套的价格进行销售,并且公司仍要负责安装调试,试问:软件公司售出多少套软件时,收入超出总费用?