设椭圆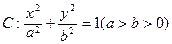
的一个顶点与抛物线
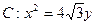的焦点重合，
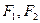分别是椭圆的左、右焦点，且离心率
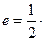且过椭圆右焦点
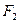的直线
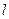与椭圆C交于
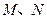两点.
（1）求椭圆C的方程；
（2）是否存在直线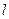，使得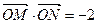
.若存在，求出直线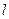的方程；若不存在，说明理由.
（3）若AB是椭圆C经过原点O的弦， MN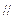
AB，求证：
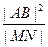为定值
已知a，b，c是全不相等的正实数，求证
。
设复数|z－i|="1," 且z¹0, z¹2i. 又复数w使
为实数，问复数w在复平面上所对应的点Z的集合是什么图形，并说明理由。
已知函数
满足下列条件：对任意的实数x1，x2都有
λ
和
，其中λ是大于0的
常数.实数a0，a，b满足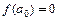 
和b=a-λf（a）.
(Ⅰ)证明:λ≤1，并且不存在
，使得
；
(Ⅱ)证明: (b-a0)2≤(1-λ2)(a-a0)2；
(Ⅲ)证明: [f(b)]2≤(1-λ2)[f(a)]2.
在对人们休闲的一次调查中，共调查了124人，其中女性70人，男性54人。女性中有43人主要的休闲方式是看电视，另外27人的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个2×2的列联表；
（2）画出三维柱形图和二维条形图；
（3）检验性别是否与休闲方式有关，可靠性有多大。
已知数列
为其前n项和，计算得
,
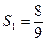,观察上述结果，推测出计算Sn的公式，并用数学归纳法加以证明。