已知函数 对一切实数x , y都满足
对一切实数x , y都满足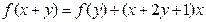 且
且 .
.
(1)求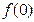 的值。 (2)求
的值。 (2)求 的解析式。
的解析式。
(3)当x∈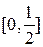 时
时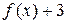 <2x+
<2x+ 恒成立,求
恒成立,求 的取值范围。
的取值范围。
车站每天8∶00~9∶00,9∶00~10∶00都恰有一辆客车到站,8∶00~9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为 ;9∶00~10∶00到站的客车B可能在9∶10,9∶30,
;9∶00~10∶00到站的客车B可能在9∶10,9∶30, 9∶50到站,其概率依次为
9∶50到站,其概率依次为 .
.
(1)旅客甲8∶00到站,设他的候车时间为 ,求
,求 的分布列和
的分布列和 ;
;
(2)旅客乙8∶20到站,设他的候车时间为 ,求
,求 的分布列和
的分布列和 .
.
已知向量 ,
, ,函数
,函数 .
.
(1)求函数 的单调递增区间
的单调递增区间
(2)在 中,
中, 分别是角
分别是角 、
、 、
、 的对边,
的对边, 且
且 ,求
,求 面积
面积 的最大值
的最大值
(本小题满分14分)
已知函数 在(0,1)内是增函数.
在(0,1)内是增函数.
(1)求实数 的取值范围;
的取值范围;
(2)若 ,求证:
,求证: .
.
(本小题满分13分)
数列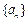 的首项
的首项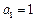 ,前
,前 项和为
项和为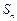 ,满足关系
,满足关系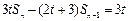 (
(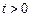 ,
,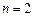 ,
, 3,4…)
3,4…)
(1)求证:数列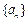 为等比数列;
为等比数列;
(2)设数列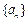 的公比为
的公比为 ,作数列
,作数列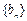 ,使
,使 ,
,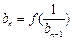 .(
.(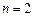 ,3,4…)求
,3,4…)求
(3)求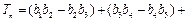 …
…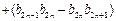 的值
的值
(本小题满分12分)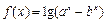 (
(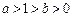 )
)
(1)求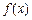 的定义域;
的定义域;
(2)问是否存在实数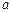 、
、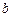 ,当
,当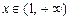 时,
时,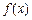 的值域为
的值域为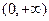 ,且
,且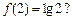 若存在,求出
若存在,求出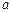 、
、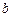 的值,若不存在,说明理由.
的值,若不存在,说明理由.