从一箱产品中随机地抽取一件产品,设事件A=“抽到的一等品”,事件B=“抽到的二等品”,事件C=“抽到的三等品”,且已知
,
,
,求下列事件的概率：⑴ 事件D=“抽到的是一等品或二等品”；⑵ 事件E=“抽到的是二等品或三等品” ．
已知二次函数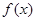
的二次项系数为
，且不等式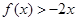
的解集为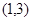
。
（1）若方程
有两个相等的根，求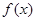的解析式；
（2）若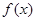的最大值为正数，求的取值范围。
函数f（x）=
的定义域为A，函数g（x）=
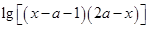的定义域为B。
（1）求A；
（2）若B
A，求实数a的取值范围。
已知函数
， 
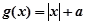
（1）当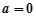
时，解不等式
；
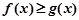（2）若存在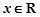
，使得
成立，求实数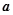
的取值范围.
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合．设点O为坐标原点, 直线
（参数
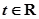）与曲线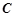
的极坐标方程为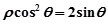 
（1）求直线l与曲线C的普通方程；
（2）设直线l与曲线C相交于A，B两点，证明：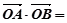
0.
如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F. 求证：
（1）
；
（2）
